Геодезическая гравиметрия
Геодезическая гравиметрия
Геодезическая гравиметрия, раздел геодезии, в котором рассматриваются теории и методы использования результатов измерения силы тяжести для решения научных и практических задач геодезии. Основное содержание Г. г. составляют теории и методы определения внешнего поля потенциала W силы тяжести g Земли по измерениям на земной поверхности S и астрономо-геодезическим материалам. Г. г. включает также теорию нивелирных высот и обработку астрономо-геодезических сетей в связи с особенностями гравитационного поля Земли. Обычно из этого поля выделяют правильное и известное поле потенциала U т. н. нормальной Земли сравнения, представляемой в виде уровенного эллипсоида. Центры масс и оси вращения реальной и нормальной Земли совпадают. Основную задачу Г. г. сводят к выводу возмущающего потенциала Т = W — U, который определяют из решения граничных задач математической физики. На земной поверхности Т удовлетворяет граничному условию
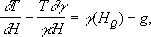
где Н — высота над эллипсоидом, g— сила тяжести в поле U, HQ — нормальная высота, выводимая из условия, что приращение (gdh потенциала W от начала счёта высот измерено в поле U, dh — элементарное превышение геометрического нивелирования. Для вывода Т разработано несколько методов, которые сводятся к решению соответствующих интегральных уравнений.
В равнинных районах некоторые практические задачи можно решать упрощёнными методами вывода Т и его производных. Эти методы основаны на условии HQ = 0, вводимом после вычисления разностей g — у (HQ). Такой подход, например, допустим при астрономо-гравиметрическом нивелировании. В этом случае задачи Г. г. будут решены в явном виде замкнутыми формулами. Значение Т на земной поверхности определяет формула Стокса (1849)
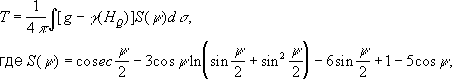
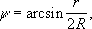R — радиус земной сферы, ds — её элемент и y— дуга большого круга между фиксированной точкой и текущей точкой, в которой задана сила тяжести. Эта формула описывает внешнее гравитационное поле земной сферы. Из неё можно вывести выражение для любого элемента гравитационного поля Земли в равнинных её областях.
Современная Г. г. основана на работах (1945—60) М. С. Молоденского и изучает способы решения граничных задач, условия их разрешимости, плотность и точность необходимых измерений.
Лит.: Молоденский М. С., Юркина М. И., Еремеев В. Ф., Методы изучения внешнего гравитационного поля и фигуры Земли, «Тр. Центрального научно-исследовательского института геодезии, аэросъёмки и картографии», 1960, в. 131; Бровар В. В., Магницкий В. А., Шимберев Б. П., Теория фигуры Земли, М., 1961.
М. И. Юркина.