69. Спецификация переменных

69. Спецификация переменных

Спецификацией переменных называется процесс отбора наиболее важных факторных переменных при построении модели регрессии.

Если в процессе эконометрического моделирования была осуществлена неправильная спецификация переменных, то это может привести к негативным последствиям, среди которых особо можно выделить два пункта:

1) из модели регрессии могут быть исключены факторные переменные, оказывающие наибольшее влияние на результативную переменную;

2) в модель регрессии могут быть включены факторные переменные, практические не связанные с результативной переменной или оказывающие на неё незначительное воздействие.

Предположим, что на основе собранных данных была построена нормальная модель множественной регрессии вида:

Y=X?+?(1)

Данную модель можно рассматривать как базисную или ограниченную модель регрессии между исследуемыми переменными.

Тогда неограниченная модель данной регрессионной зависимости будет иметь вид:

Y=X?+Z?+?(2)

где Y – вектор результативных переменных;

X – вектор количественных факторных переменных;

Z – некоторая фиктивная переменная;

?, ? – вектор неизвестных коэффициентов модели регрессии без ограничений, подлежащих оцениванию.

Рассмотрим случай исключения факторных переменных, оказывающих наибольшее влияние на результативную переменную, из модели регрессии.

Предположим, что модель регрессии с ограничениями является значимой. Исходя из этого условия, рассчитаем оценку коэффициента ?, полученную методом наименьших квадратов, в оцениваемой модели регрессии с ограничениями (1):

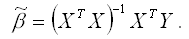
Подставим в данную формулу вместо Y выражение X?+Z?+?:

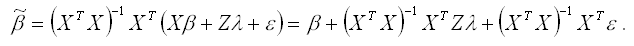
Охарактеризуем полученную оценку коэффициента ? модели регрессии с ограничениями с точки зрения свойства несмещённости. Для этого рассчитаем математическое ожидание оценки

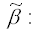
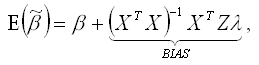
где BIAS – это смещение оценки коэффициента ?.

Таким образом, оценка

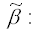
является смещённой, и устранить эту смещённость невозможно, даже при условии увеличения объёма выборочной совокупности.

Оценка коэффициента ? модели регрессии с ограничениями (1) будет обладать свойством несмещённости в двух случаях:

1) если коэффициент при фиктивной переменной Z будет равен нулю:

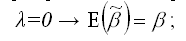
2) при условии, что пропущенные переменные будут ортогонально включены в модель:

XTZ = 0.

Рассчитаем ковариацию оценки коэффициента ? модели регрессии с ограничениями (1):

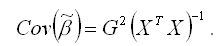
Матрица ковариаций МНК-оценок принимает такой вид только в том случае, если модель (1) является значимой.

Рассмотрим случай, когда в модель регрессии могут быть включены факторные переменные, практические не связанные с результативной переменной или оказывающие на неё незначительное воздействие.

Предположим, что модель регрессии без ограничений (2) является значимой. Исходя из этого условия, оценим коэффициенты модели регрессии с ограничениями (1).

Представим регрессионную модель с ограничениями (1) в следующем виде:

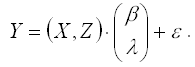
Пусть W – это переменные (X,Z) модели регрессии. Тогда оценка коэффициента ? модели регрессии без ограничений может быть записана следующим образом:

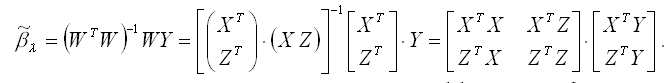
Охарактеризуем полученную оценку коэффициента ? модели регрессии без ограничений с точки зрения свойства несмещённости. Для этого рассчитаем математическое ожидание оценки

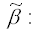
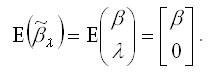
Следовательно, оценка

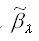
является несмещённой оценкой коэффициента регрессии ? модели (2). Если в данную модель включить один дополнительный фактор, то оценки уже включённых факторных переменных свойства несмещённости не утратят. Но если в модель регрессии будут включены много лишних параметров, то точность оценок будет падать.

Матрица ковариаций МНК-оценок модели регрессии без ограничений будет иметь вид:

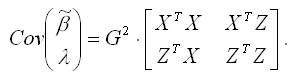
Матрица ковариаций будет иметь такой вид только в случае значимости модели регрессии без ограничений.

Данный текст является ознакомительным фрагментом.