78. Одномерный анализ Фурье

78. Одномерный анализ Фурье

Одним из основных методов моделирования сезонных и циклических колебаний является метод, основанный на применении одномерных рядов Фурье. В свою очередь, ряды Фурье являются одной из разновидностей спектрального анализа.

С помощью спектрального анализа в структуре временного ряда определяется пик отклонений от тренда, что позволяет рассчитать длительность периодической компоненты ряда.

Для того, чтобы к временному ряду можно было применять методы спектрального анализа, его необходимо привести к стационарному виду.

Суть спектрального анализа заключается в том, что случайный стационарный процесс представляется как сумма гармонических колебаний различных частот, называемых гармониками.

Спектром называется функция, которая описывает распределение амплитуд случайного стационарного процесса по различным частотам.

Сезонная компонента временного ряда может быть разложена в ряд Фурье.

Сезонные колебания, разложенные рядом Фурье, представляют собой сумму нескольких синусоидальных и косинусоидальных гармоник с различными периодами:

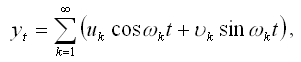
где uk, ?k – некоррелированные случайные величины с нулевым математическим ожиданием и одинаковыми дисперсиями:

D(uk)=D(?k)=Dk;

?k– длина волны функции синуса или косинуса, называемая частотой.

Частота выражается числом циклов (периодов) в единицу времени.

Цель спектрального анализа временных рядов заключается в оценивании спектра ряда. Спектр временного ряда можно определить как разложение дисперсии ряда по частотам для определения значимых гармоник.

Значение спектра временного ряда рассчитывается по формуле:

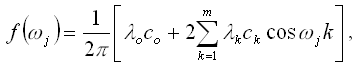
где ?j – частоты, для которых оцениваются спектры:

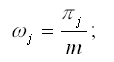
ck – автокорреляционная функция, значения которой рассчитываются по формуле:

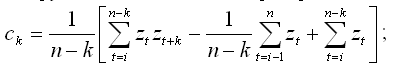
?k – специально подобранные веса значений ковариационной функции, зависящие от частоты m, которые называются корреляционным окном.

Корреляционным окном называется преобразованная форма взвешенного скользящего среднего шириной m.

Дисперсия ряда Фурье рассчитывается по формуле:

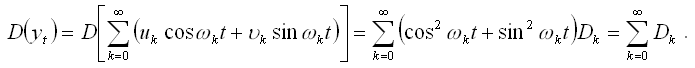
Дисперсия ряда Фурье равна сумме всех гармоник её спектрального разложения.

Следовательно, дисперсия D(yt) распределена по различным частотам. Графически распределение дисперсии ряда Фурье изображается с помощью периодограммы. Суть анализа периодограммы заключается в определении частоты или периода с наибольшими спектральными плотностями, которые вносят наибольший вклад в периодические колебания временного ряда, что позволит определить его основной период колебания.

Ряд Фурье вида

можно рассматривать как линейную модель множественной регрессии.

Результативной переменной в данной модели будут являться значения временного ряда, а независимыми переменными – функции синусов всех возможных частот. Коэффициенты uk при косинусах и ?k  при синусах будут представлять собой коэффициенты модели регрессии, которые показывают степень, с которой коррелированности соответствующих функций с исходными данными. Если рассчитанное значение коэффициента при определённом синусе или косинусе достаточно велико, то на соответствующей частоте в исходных данных существует строгая периодичность.