85. Критерий Дикки-Фуллера проверки наличия единичных корней

85. Критерий Дикки-Фуллера проверки наличия единичных корней

Проверкой наличия единичных корней называется задача проверки основной гипотезы вида

H0:?=0 в модели авторегрессии первого порядка:

yt=a+?yt–1+?t.

Для данного ряда справедливы следующие предположения:

1) временной ряд yt является стационарным, если выполняется условие – 1‹?‹1;

2) временной ряд yt является нестационарным и представляет собой модель со случайным трендом, если выполняется условие ?=1;

3) временной ряд yt также является нестационарным, если выполняется условие ?›0.

Таким образом, гипотеза о стационарности временного ряда yt состоит в проверке основной гипотезы вида H0:?=1.

Критерий Дикки-Фуллера используется при проверке гипотезы о наличия единичных корней.

При этом выдвигается основная гипотеза вида H0:?=1 для модели авторегрессии первого порядка:

yt=a+?yt–1+?t.

Однако на следующем этапе оценивается не эта модель авторегрессии, а модель, которая получается после перехода к первым разностям:

?yt=?yt-1+?t,

где ?=?–1.

Проверка основной гипотезы вида H0:?=1 для исходной модели авторегрессии первого порядка аналогична проверке гипотезы H0:?=0 для полученной модели. Проверка данной гипотезы может осуществляться для трёх типов регрессионных уравнений:

?yt=?yt-1+?t;(1)

?yt=а+?yt-1+?t; (2)

?yt=а+?yt-1+?t+?t. (3)

Данные модели регрессии отличаются только наличием членов модели a и ?t.

Первая модель является моделью случайного тренда, во вторую модель включается свободный член a, являющийся коэффициентом случайного тренда. В третью модель включены и коэффициент случайного тренда, и коэффициент линейного временного тренда ?t.

Проверка основной гипотезы H0:?=0 состоит в оценивании методом наименьших квадратов одной или нескольких из моделей регрессии 1, 2, 3 для получения оценки  и её стандартной ошибки.

Наблюдаемое значение t-критерия для проверки основной гипотезы вида H0:?=0  состоит в оценивании методом наименьших квадратов одной или нескольких из моделей регрессии 1, 2, 3 для получения оценки

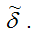
и её стандартной ошибки.

Наблюдаемое значение t-критерия для проверки основной гипотезы вида H0:?=0 рассчитывают по формуле:

где

– стандартная ошибка оценки

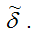
Однако критическое значение t-критерия в данном случае нельзя определить по таблице распределения Стьюдента. Дикки и Фуллер провели исследования, в результате которых определили критические значения t-критерия для проверки гипотезы H0:?=0 в зависимости от вида модели регрессии и объёма выборочной совокупности. Данные статистики обозначаются как ? – для первой модели регрессии, ?? – для второй модели регрессии, ?х – для третьей модели регрессии. Они приведены в таблице критических значений статистик Дикки-Фуллера для различных уровней значимости.

При проверке гипотезы о наличии во временном ряду авторегрессии более чем первого порядка используется расширенный критерий Дикки-Фуллера (Augmented Dickey-Fuller Test – ADF).

Процесс авторегрессии порядка р можно записать следующим образом:

Основная гипотеза формулируется как H0:?=0. Если данная гипотеза верна, то данная модель авторегрессии имеет единичный корень, т. е. подчиняется процессу авторегрессии первого порядка.

Проверка основной гипотезы H0:?=0 осуществляется для различных типов регрессионных уравнений:

Справедливость основной гипотезы проверяется с помощью статистики ? для первой модели регрессии (при отсутствии свободного члена и временного тренда).

Справедливость основной гипотезы проверяется с помощью статистики ?? для второй модели регрессии, включающей свободный член.

Справедливость основной гипотезы проверяется с помощью статистики ?х для третьей модели регрессии, включающей свободный член и временной линейный тренд.

Если сумма коэффициентов модели регрессии вида

равна единице, т. е.

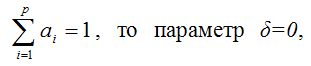
 т. е. в данной модели имеется единичный корень.

Данный текст является ознакомительным фрагментом.