Гамильтона оператор

Гамильто'на опера'тор, набла оператор, Ñ-оператор, дифференциальный оператор вида

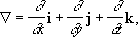
  где i, j, k — координатные орты. Введён У. Р. Гамильтоном (1853). Если Г. о. применить к скалярной функции j(x, у, z), понимая Ñj как произведение вектора на скаляр, то получится градиент функции j(x, у, z) :

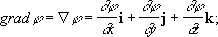
  если применить Г. о. к векторной функции r (x, у, z), понимая Dr как скалярное произведение векторов, то получится дивергенция вектора r:

  (u, v и w — координаты вектора r ). Скалярное произведение Г. о. самого на себя даёт Лапласа оператор .