1.3.3. Система управления БАК
1.3.3. Система управления БАК
Всю систему автоматического управления авиационным комплексом (АК) можно представить в виде иерархической структуры, показанной на рис. 1.89. Здесь стрелками показаны сигналы: управляющие (сверху вниз) и информационные (снизу вверх). На рисунке показаны три уровня автоматического управления АК и модели, используемые при формировании управляющих воздействий, а также верхний уровень управления, всю работу на котором выполняет человек-оператор. Следует отметить, что оператор, как правило, имеет возможность управлять любым из низлежащих уровней, задавая:
– текущую задачу для СУАК;
– действие для конкретного БПЛА;
– требуемое значение какого-либо параметра состояния БПЛА.
При этом всю необходимую информацию о состоянии компонентов БАК (помимо визуальной из окружающего пространства) оператор получает через средства отображения информации (СОИ), как правило, входящие в состав СУАК.
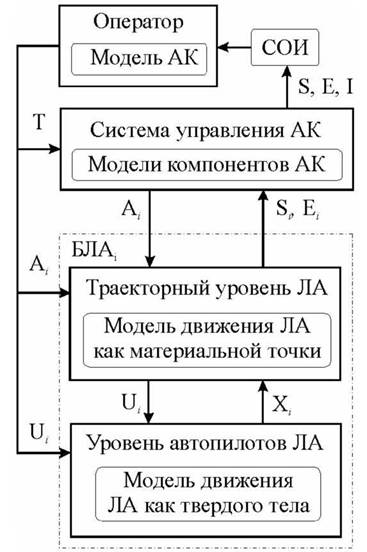
Рис. 1.89. Уровни управления авиационным комплексом
На уровне оператора используется модель авиационного комплекса, включающая описание:
– задач, которые способен выполнять комплекс;
– условий применения и областей достижимости АК;
– имеющихся ЛA, их полезной нагрузки и центральной системы управления комплексом;
– коммуникаций между компонентами комплекса.
Модель АК как средства для решения некоторого множества задач можно представить следующим образом:
Mod (1) = {T,E,R}, (1.1)
где Т =(Т1,Т2 …,Тq) – множество задач, выполняемых комплексом;
Е = (Е1, Е2 ..., Ej)– параметры состояния окружающей среды (условия применения комплекса);
R = (R1,R2 ,…,Rn ) – множество компонентов, составляющих АК: ЛA, взлетно-посадочные устройства; устройства связи и управления.
На этом уровне решаются следующие задачи:
– назначение задачи сеанса функционирования АК;
– назначение конкретных ЛA для использования;
– обозначение основных ограничений и дополнительных условий.
Критерием качества управления на этом уровне может служить способность БАК выполнить поставленную задачу (совокупность задач) в определенных условиях за ограниченное время (t ‹= tзад )
I(1) = {T,E,t}.
Система управления АК может иметь различное базирование [66], но наземное расположение является самым простым и распространенным. На этом уровне используются модели описания:
– ЛA в составе комплекса, их основных ЛTX и функциональных возможностей, а также динамических характеристик других подвижных компонентов;
– назначенной задачи сеанса функционирования комплекса;
– количества ЛA, а также степень возможной замены одних компонентов (например, вышедших из строя) другими. Модель АК как совокупности разнородных компонентов, решающих свои собственные задачи в рамках общей стоящей перед комплексом цели можно представить следующим образом:
Mod(2) = {S,A,J,E}, (1-2)
где S = (S1,S2 ,…,Sn ) – множества параметров состояний компонентов комплекса, прежде всего координат их местонахождения;
A = (A1 ,A2 ,…,An) – множества действий компонентов, включая алгоритмы решения типовых задач из множества Т;
J = (J1,J2 ,…,Jn ) – множества, характеризующие каждый компонент в качестве исполнителя подзадач из множества Т. При этом необходимо учесть летно-технические характеристики имеющихся БПЛА и их целевой нагрузки для выполнения конкретной задачи [74].
Решаемые задачи:
– построение решения поставленной перед АК задачи в виде совокупности подзадач, решаемых каждым ЛА в составе комплекса;
– составление плана полета для каждого ЛA, а также перечня действий в определенных точках с учетом топливновременных ограничений;
– согласование движения нескольких ЛА в составе АК, если это необходимо.
Критерий качества управления на этом уровне можно сформулировать как оценку решения каждым БПЛА поставленной перед ним задачи с определенным уровнем эффективности:
I(2) = {T,J}
Следующие два уровня реализуются непосредственно на борту ЛА. Соответственно, перечисленные ниже характеристики могут иметь количественные различия в зависимости от типоразмера и выполняемой ЛА задачи.
Траекпгорный уровень управления содержит подробное описание движения ЛА, в том числе и возможный разброс значений основных параметров при их выполнении. Таким образом, модели этого уровня содержат следующие сведения:
– математическое описание пространственного движения ЛА как материальной точки;
– предельные значения скоростей и эйлеровых углов при выполнении типовых маневров;
– требования к точности выдерживания заданной траектории;
– требования к выдерживанию определенных дистанций между несколькими одновременно выполняющими полет ЛА.
Модель компонента АК (летательного аппарата), как материальной точки, выполняющей определенные действия в окружающей среде, можно представить следующим образом:
Mod(0) = {Sj ,Aj ,E}, (1.3)
где Sj=(s1j,s2j,…,smj ) – параметры состояния компонента
Rj , j = 1,n
т – количество переменных, описывающих состояние компонента;
Aj =(a1j,a2j,…,ahj ) – действия, которые может выполнять компонент комплекса Rj для изменения окружающей среды и собственного состояния;
h – количество таких действий.
Решаемые задачи:
– расчет конкретных значений параметров типовых участков траекторий исходя из ЛTX ЛA и специфики решаемой задачи;
– предотвращение опасных сближений и потерь ЛА;
– обеспечение выполнения запланированных действий на каждом участке траектории.
Эффективность управления на этом уровне можно сформулировать как отработку заданных действий за заданное время с заданной точностью (Q):
I(3) = {A,Q,t}.
На нижнем уровне управления обеспечивается отработка всех действий ЛА, рассчитанных на траекторном уровне. Соответственно, модель этого уровня содержит:
– математическое описание пространственного движения ЛА как твердого тела;
– законы управления отдельными параметрами движения ЛА;
– предельные значения некоторых величин, подлежащих ограничению.
Модель ЛА, как объекта управления, можно представить в следующем виде:
Mod(4) = {Uj ,Xj,Sj} (1.4)
где Uj – множество управляющих воздействий;
Xj – множество выходных параметров.
Решаемые задачи:
– формирование управляющих воздействий, передающихся для отработки в САУ;
– ограничение предельных значений заданных величин.
Задачи этого уровня решаются традиционными методами теории автоматического управления, поэтому качество их решения может быть выражено показателями качества переходных процессов всех задействованных САУ:
I(4) = {?,tрег,?},
где ? – перерегулирование;
tрег – время регулирования;
? – статическая точность.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
НОВАЯ СИСТЕМА ГОСУДАРСТВЕННОГО УПРАВЛЕНИЯ
НОВАЯ СИСТЕМА ГОСУДАРСТВЕННОГО УПРАВЛЕНИЯ Как новую систему государственного управления определяют в Великобритании результат проведения серии реформ, цель которых состояла в смене модели реализации государственной политики и выразившихся в раздроблении системы
Автоматизированная система управления
Автоматизированная система управления Автоматизированная система управления – совокупность экономико-математических методов, измерительных устройств, средств связи, устройств отображения информации, передачи данных и организационных комплексов, которые включают в
Активная система управления ориентацией
Активная система управления ориентацией Активная система управления ориентацией – система ориентации, входящая в состав космического аппарата и обеспечивающая выработку управляющих моментов. Принцип работы состоит в обработке показаний гиросистемы и датчиков
1.3.3. Система управления БАК
1.3.3. Система управления БАК Всю систему автоматического управления авиационным комплексом (АК) можно представить в виде иерархической структуры, показанной на рис. 1.89. Здесь стрелками показаны сигналы: управляющие (сверху вниз) и информационные (снизу вверх). На рисунке