83. Модель авторегрессии и проинтегрированного скользящего среднего

83. Модель авторегрессии и проинтегрированного скользящего среднего

Модель авторегрессии и проинтегрированного скользящего среднего (АРПСС) была предложена американскими учёными Боксом и Дженкинсом в 1976 г. как один из методов оценки неизвестных параметров и прогнозирования временных рядов.

Моделью авторегрессиии проинтегрированного скользящего среднего называется модель, которая применяется при моделировании нестационарных временных рядов.

Нестационарный временной ряд характеризуется непостоянными математическим ожиданием, дисперсией, автоковариацией и автокорреляцией.

В основе модели авторегрессии и проинтегрированного скользящего среднего лежат два процесса:

1) процесс авторегрессии;

2) процесс скользящего среднего.

Процесс авторегрессии может быть представлен в виде:

xt=a+?1xt-1+?2xt-2+…+?t,

где a – свободный член модели, являющийся константой;

?1 ?2…— параметры модели авторегрессии;

? – случайное воздействие (ошибка модели).

Каждое наблюдение в модели авторегрессии представляет собой сумму случайной компоненты и линейной комбинации предыдущих наблюдений.

Процесс скользящего среднего может быть представлен в виде:

xt=?+?t–?1?t–1–?2?t–2–…

где ? – свободный член модели, являющийся константой;

?1 ?2… – параметры модели скользящего среднего;

? – случайное воздействие (ошибка модели).

Текущее наблюдение в модели скользящего среднего представляет собой сумму случайной компоненты в данный момент времени и линейной комбинации случайных воздействий в предыдущие моменты времени.

Следовательно, в общем виде модель авторегрессии и проинтегрированного скользящего среднего описывается формулой:

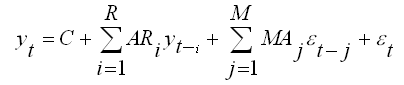
где С – свободный член модели, являющийся константой;

?t – некомпенсированный моделью случайный остаток.

В обозначениях Бокса и Дженкинса модель авторегрессии и проинтегрированного скользящего среднего записывается как АРПСС(p,d,q) или ARIMA (p,d,q), где

p – параметры процесса авторегрессии;

d – порядок разностного оператора;

q – параметры процесса скользящего среднего.

Для рядов с периодической сезонной компонентой применяется модель авторегрессии и проинтегрированного скользящего среднего с сезонностью, которая в обозначениях Бокса и Дженкинса записывается как АРПСС (p,d,q) (ps,ds,qs), где

ps – сезонная авторегрессия;

ds – сезонный разностный оператор;

qs – сезонное скользящее среднее.

Моделирование нестационарных временных рядов с помощью модели авторегрессии и проинтегрированного скользящего среднего осуществляется в три этапа:

1) проверка временного ряда на стационарность;

2) идентификация порядка модели и оценивание неизвестных параметров;

3) прогноз.

Применение модели АРПСС предполагает обязательную стационарность исследуемого ряда, поэтому на первом этапе данное предположение проверяется с помощью автокорреляционной и частной автокорреляционной функций ряда остатков. Остатки представляют собой разности наблюдаемого временного ряда и значений, вычисленных с помощью модели.

Устранить нестационарность временного ряда можно с помощью метода разностных операторов.

Разностным оператором первого порядка называется замена исходного уровня временного ряда разностями первого порядка:

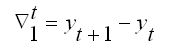
Разностные операторы первого порядка позволяет исключить линейные тренды.

Разностные операторы второго порядка позволяют исключить параболические тренды.

Сезонные разностные операторы предназначены для исключения 12-ти или 4-х периодичной сезонности:

Если модель содержит и трендовую, и сезонную компоненты, то необходимо применять оба оператора.

На втором этапе необходимо решить, сколько параметров авторегрессии и скользящего среднего должно войти в модель.

В процессе оценивания порядка модели авторегрессии и проинтегрированного скользящего среднего применяется квазиньютоновский алгоритм максимизации правдоподобия наблюдения значений ряда по значениям параметров. При этом минимизируется (условная) сумма квадратов остатков модели. Для оценки значимости параметров используется t-статистика Стьюдента. Если значения вычисляемой t-статистики не значимы, соответствующие параметры в большинстве случаев удаляются из модели без ущерба подгонки.

Полученные оценки параметров используются на последнем этапе для того, чтобы вычислить новые значения ряда и построить доверительный интервал для прогноза.

Оценкой точности прогноза, сделанного на основе модели авторегрессии и проинтегрированного скользящего среднего является среднеквадратическая ошибка (mean square), вычисляемая по формуле:

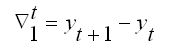
Чем меньше данный показатель, тем точнее прогноз.

Модель авторегрессии и проинтегрированного скользящего среднего считается адекватной исходным данным, если остатки модели являются некоррелированными нормально распределёнными случайными величинами.

Данный текст является ознакомительным фрагментом.