84. Показатели качества модели авторегрессии и проинтегрированного скользящего среднего
84. Показатели качества модели авторегрессии и проинтегрированного скользящего среднего
Основными показателями качества модели авторегрессии и проинтегрированного скользящего среднего являются критерий Акайка и байесовский критерий Шварца. Данные критерии аналогичны критерию максимума скорректированного множественного коэффициента детерминации R2или минимума дисперсии случайной ошибки модели G2.
Информационный критерий Акайка (Akaike information criterion – AIC) используется для выбора наилучшей модели для временного ряда yt из некоторого множества моделей.
Предположим, что с помощью метода максимального правдоподобия была получена оценка
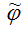
вектора неизвестных параметров модели ?. Обозначим через
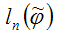
максимальное значение логарифмической функции правдоподобия эконометрической модели.
Тогда критерий Акайка можно будет представить в виде:
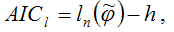
где h – размерность вектора неизвестных параметров модели ?.
Для линейной или нелинейной модели регрессии, включающей только одно уравнение, критерий Акайка может быть преобразован к виду:
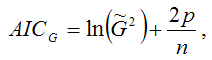
где n – объём выборочной совокупности;
– оценка максимального правдоподобия дисперсии остатков etмодели регрессии.
Оба варианта критерия Акайка дают одинаковый результат, но в первом случае выбирается модель с наибольшим значением критерия, а во втором случае – с наименьшим значением критерия.
Байесовский критерий Шварца (Schwarz Bayesian criterion – SBC) также используется для выбора наилучшей модели временного ряда из некоторого множества моделей.
Байесовский критерий Шварца для временных рядов можно представить в виде:
Байесовский критерий Шварца для моделей регрессии можно представить в виде:
По первому варианту расчёта критерия Байесовского критерий Шварца SBC выбирается та модель, для которой значение SBCt является наибольшим. При втором варианте выбирается та модель, для которой значение SBCG является наименьшим.
При проверке качества моделей результаты критериев Акайка и Шварца могут быть различны.
Общий критерий множителей Лагранжа (LM-test) применяется для проверки качества модели авторегрессии и проинтегрированного скользящего среднего с помощью автокорреляции остатков. С помощью данного критерия можно обнаружить в остатках регрессии автокорреляцию более высоких порядков, чем первый, но при этом необходимо, чтобы выборочная совокупность была достаточно велика.
Предположим, что на основании собранных данных была построена модель регрессии вида:
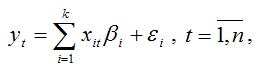
где ?t – случайная ошибка модели:
?t=?1?t–1+?2?t–2+…+?p?t-p+ut;
? – коэффициент автокорреляции порядка (1…?);
ut – нормально распределённая случайная величина с нулевым математическим ожиданием и дисперсией G2: ut ~N(0,G2).
Данная модель регрессии может в качестве факторных переменных включать лаговые значения зависимой переменной. Поэтому необходимо проверить основную гипотезу H0 о незначимости коэффициентов автокорреляции:
H0:?1=?2=…=?p=0.
Альтернативная гипотеза формулируется как утверждение о значимости коэффициентов автокорреляции:
H1:?1??2?…??p?0.
Проверка выдвинутых гипотез осуществляется с помощью общего критерия множителей Лагранжа в несколько этапов:
1) оценки неизвестных коэффициентов модели регрессии вида
рассчитываются с помощью метода наименьших квадратов;
2) рассчитываются остатки модели регрессии et:
3) определяются оценки модели регрессия вида:
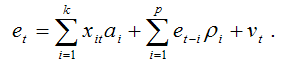
Для данной модели осуществляется проверка значимости коэффициентов ?i при лаговых значениях остатков. Для этого вычисляется F-статистика, которая распределена по ?2 закону распределения с p степенями свободы. Если наблюдаемое значение ?2-критерия больше критического значения ?2-критерия, т. е.
то основная гипотеза об отсутствии автокорреляции в остатках отвергается. Если наблюдаемое значение ?2-критерия меньше критического значения ?2-критерия, т. е.
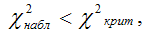
то гипотеза об отсутствии автокорреляции принимается.
Данный текст является ознакомительным фрагментом.