95. Модели авторегрессии

95. Модели авторегрессии

Моделью авторегрессии называется динамическая эконометрическая модель, в которой в качестве факторных переменных содержатся лаговые значения результативной переменной.

Пример модели авторегрессии:

yt=?0+?1xt+?1yt–1+?t,

где ?1 – это коэффициент, который характеризует краткосрочное изменение переменной у под влиянием изменения переменной х на единицу своего измерения;

?1 – это коэффициент, который характеризует изменение переменной у в текущий момент времени t под влиянием своего изменения в предыдущий момент времени (t–1).

Промежуточным мультипликатором называется произведение коэффициентов модели авторегрессии (?1*?1).

Промежуточный мультипликатор отражает общее абсолютное изменение результативной переменной у в момент времени (t+1).

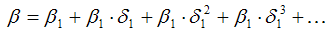
Определение. Долгосрочным мультипликатором называется показатель, рассчитываемый как

Долгосрочный мультипликатор отражает общее абсолютное изменение результативной переменной у в долгосрочном периоде.

Если для модели авторегрессии выполняется условие |?|<1, то при наличии бесконечного лага будет справедливым равенство:

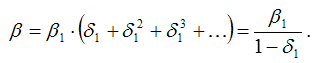
В нормальной линейной модели регрессии все факторные переменные не зависят от случайной ошибки модели. Данное условие для моделей авторегрессии нарушается, потому что переменная yt-1 частично зависит от случайной ошибки модели ?t. Следовательно, при оценке неизвестных коэффициентов традиционным методом наименьших квадратов ы получим смещённую оценку коэффициента при переменной yt–1.

При определении оценок неизвестных коэффициентов модели авторегрессии используется метод инструментальных переменных (IV – Instrumental variables).

Суть метода инструментальных переменных заключается в том, что переменная yt–1, для которой нарушается предпосылка применения метода наименьших квадратов, заменяется на новую переменную z, удовлетворяющую двум требованиям:

1) данная переменная должна тесно коррелировать с переменной yt–1: cov(yt–1,z)?0;

2) данная переменная не должна коррелировать со случайной ошибкой модели ?t: cov(z,?)=0.

Предположим, что на основании собранных данных была построена модель авторегрессии вида:

yt=?0+?1xt+?1yt–1+?t.

Рассчитаем оценки неизвестных коэффициентов данной модели с помощью метода инструментальных переменных.

В данной модели авторегрессии переменная yt коррелирует с переменной xt, следовательно, переменная yt–1 зависит от переменной xt–1. Охарактеризуем данную корреляционную зависимость с помощью парной модели регрессии вида:

yt–1=k0+k1xt–1+ut,

где k0 ,k1 – неизвестные коэффициенты модели регрессии;

ut – случайная ошибка модели регрессии.

Обозначим выражение k0+k1xt–1 через переменную zt–1. Тогда модель регрессии для переменной yt–1 примет вид:

yt–1= zt–1+ut.

Новая переменная zt–1  удовлетворяет свойствам, предъявляемым к инструментальным переменным:

1) она тесно коррелирует с переменной yt–1: cov(zt–1,yt–1)?0;

2) она коррелирует со случайной ошибкой исходной модели авторегрессии ?t:  cov(?t, zt–1).

Таким образом, исходная модель авторегрессии может быть представлена следующим образом:

yt=?0+?1xt+?1(k0+k1xt–1+ut)+?t= ?0+?1xt+?1 zt–1+?t,

где ?t= ?1 ut+ ?t.

На следующем этапе оценки неизвестных коэффициентов преобразованной модели рассчитываются с помощью традиционного метода наименьших квадратов. Эти оценки будут являться оценками неизвестных коэффициентов исходной модели авторегрессии.

Данный текст является ознакомительным фрагментом.