71. Метод проверки гипотезы о существовании тренда во временном ряду, основанный на сравнении средних уровней ряда

71. Метод проверки гипотезы о существовании тренда во временном ряду, основанный на сравнении средних уровней ряда

Наличие во временном ряду трендовой компоненты не всегда можно определить с помощью графика. Поэтому для выявления этой компоненты используются специальные критерии проверки гипотезы о существовании тренда во временном ряду.

Рассмотрим следующие критерии проверки гипотезы о существовании тренда во временном ряду:

1) критерий, основанный на сравнении средних уровней временного ряда;

2) критерий «восходящих и нисходящих» серий;

3) критерий серий, основанный на медиане выборочной совокупности.

При проверке гипотезы о существовании тренда во временном ряду с помощью критерия, основанного на сравнении средних уровней, временной ряд из N наблюдений делится на две равные части. Объём первой части yi равен

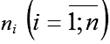
и объём второй части yj равен

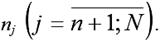
Обе части временного ряда рассматриваются как самостоятельные выборочные совокупности, подчиняющиеся нормальному закону распределения.

Для каждой из выборок yi и yj рассчитываются следующие выборочные характеристики:

1) средние арифметические значения:

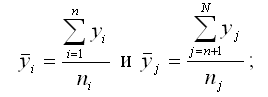
2) выборочные дисперсии:

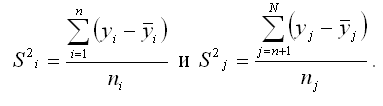
При проверке предположения о наличии во временном ряду трендовой компоненты выдвигается основная гипотеза о равенстве генеральных средних для двух образованных выборочных совокупностей:

H0:?i=?j.

Альтернативной или обратной является гипотеза о неравенстве генеральных средних для двух образованных выборочных совокупностей:

H0:?i??j.

Основная гипотеза вида H0:?i=?j проверяется при справедливости предположения о равенстве генеральных дисперсий:

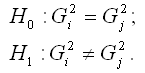
Гипотеза о равенстве дисперсий проверяется с помощью F-критерия Фишера.

Наблюдаемое значение F-критерия сравнивают с критическим значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора.

Критическое значение F-критерия Фишера определяется по таблице распределения Фишера-Снедекора в зависимости от уровня значимости а и двух степеней свободы

k1=n–1 и k2=N–n–2.

Наблюдаемое значение F-критерия при проверке основной гипотезы вида  

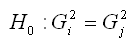
определяется по формуле:

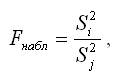
при условии, что

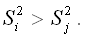
При проверке выдвинутых гипотез возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл>Fкрит, то основная гипотеза отклоняется.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т.е. Fнабл?Fкрит, то основная гипотеза принимается.

Гипотеза о равенстве генеральных средних проверяется с помощью t-критерия Стьюдента.

Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.

Критическое значение t-критерия tкрит(а,N–2) определяется по таблице распределения Стьюдента, где а – уровень значимости, (N–2) – число степеней свободы.

Наблюдаемое значение t-критерия при проверке основной гипотезы вида H0:?i=?j определяется по формуле:

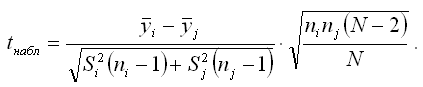
При проверке гипотез возможны следующие ситуации.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. tнабл>tкрит, то основная гипотеза отвергается, и генеральные средние двух выборок не равны между собой. Следовательно, в исходном временном ряду присутствует трендовая компонента.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. tнабл?tкрит, то основная гипотеза принимается, и генеральные средние двух выборок равны между собой. Следовательно, в исходном временном ряду отсутствует трендовая компонента.

Данный текст является ознакомительным фрагментом.