27. Классический метод наименьших квадратов для модели множественной регрессии. Метод Крамера
27. Классический метод наименьших квадратов для модели множественной регрессии. Метод Крамера
В общем виде линейную модель множественной регрессии можно записать следующим образом:
yi=?0+?1x1i+…+?mxmi+?i,
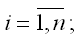
где yi – значение i-ой результативной переменной,
x1i…xmi – значения факторных переменных;
?0…?m – неизвестные коэффициенты модели множественной регрессии;
?i – случайные ошибки модели множественной регрессии.
В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Суть метода наименьших квадратов состоит в том, чтобы найти такой вектор ? оценок неизвестных коэффициентов модели, при которых сумма квадратов отклонений (остатков) наблюдаемых значений зависимой переменной у от расчётных значений ? (рассчитанных на основании построенной модели регрессии) была бы минимальной.
Матричная форма функционала F метода наименьших квадратов:
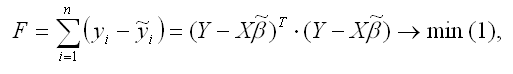
где
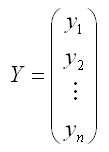
– случайный вектор-столбец значений результативной переменной размерности (n*1);
– матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент ?0 умножается на единицу;
В процессе минимизации функции (1) неизвестными являются только значения коэффициентов ?0…?m, потому что значения результативной и факторных переменных известны из наблюдений. Для определения минимума функции (1) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (1):
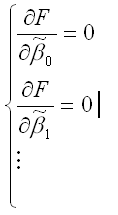
где
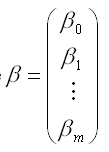
– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);
Общий вид стационарной системы уравнений для функции (1):
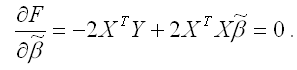
Решением стационарной системы уравнений будут МНК-оценки неизвестных параметров линейной модели множественной регрессии:
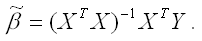
Оценим с помощью метода наименьших квадратов неизвестные параметры линейной модели двухфакторной регрессии:
yi=?0+?1x1i+?2x2i+?i,
где
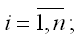
Чтобы рассчитать оценки неизвестных коэффициентов ?0,?1 и ?2 данной двухфакторной модели регрессии, необходимо минимизировать функционал F вида:
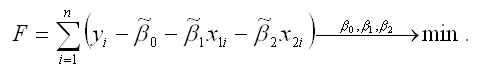
Для определения экстремума функции нескольких переменных, частные производные по этим переменным приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для модели множественной линейной регрессии с двумя переменными:
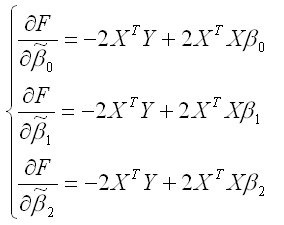
В результате элементарных преобразований данной стационарной системы уравнений получим систему нормальных уравнений:
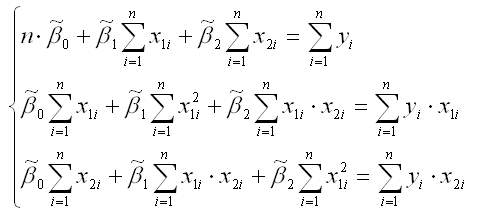
Данная система называется системой нормальных уравнений относительно коэффициентов
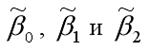
для модели регрессии yi=?0+?1x1i+?2x2i+?i.
Полученная система нормальных уравнений является квадратной, т. к. количество уравнений равняется количеству неизвестных переменных, поэтому коэффициенты
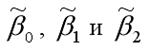
можно рассчитать с помощью метода Крамера или метода Гаусса.
Рассмотрим подробнее метод Крамера решения квадратных систем нормальных уравнений.
Единственное решение квадратной системы линейных уравнений определяется по формуле:
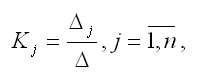
где ? – основной определитель квадратной системы линейных уравнений;
?j – определитель, полученный из основного определителя путём замены j-го столбца на столбец свободных членов.
При использовании метода Крамера возможно возникновение следующих ситуаций:
1) если основной определитель системы ? равен нулю и все определители ?jтакже равны нулю, то данная система имеет бесконечное множество решений;
2) если основной определитель системы ? равен нулю и хотя бы один из определителей ?jтакже равен нулю, то система решений не имеет.
Данный текст является ознакомительным фрагментом.