52. Метод наименьших квадратов для двухфакторной производственной функции Кобба-Дугласа. Эффект от масштаба производства

52. Метод наименьших квадратов для двухфакторной производственной функции Кобба-Дугласа. Эффект от масштаба производства

Двухфакторную производственную функцию Кобба-Дугласа f(K,L) можно представить в виде:

Q=A*Ka*L?,

где Q – объём выпущенной продукции (в стоимостном или натуральном выражении);

K – объём основного капитала или основных фондов;

L – объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней).

A,a,? – неизвестные числовые параметры производственной функции, которые подчиняются условиям:

1) 0?а?1;

2) 0???1;

3) A›0;

4) a+?=1.

Двухфакторная производственная функция Кобба-Дугласа относится к классу нелинейных по параметрам функций, которые можно свести к линейному виду.

Для того, чтобы привести двухфакторную производственную функцию Кобба-Дугласа к линейному виду, необходимо прологарифмировать обе части данной функции:

lnQj–lnLj=lna+?(lnKj–lnLj)+?j,,

где ?j – случайная ошибка производственной функции

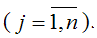
Для более наглядного представления данной модели регрессии воспользуемся методом замен:

yj= lnQj–lnLj;

b0=lna;

b1=?;

b=[ b0 b1]T;

xj= lnKj–lnLj;

?T(xj)=[0 xj].

В результате произведённых замен получим окончательный вид производственной функции Кобба-Дугласа, приведённой к линейной форме:

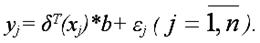
В данной функции неизвестным является только вектор коэффициентов b. Оценку данного вектора можно получить с помощью классического метода наименьших квадратов по формулам: 

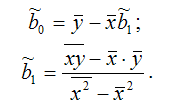
где

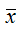
– среднее арифметическое значение переменной х: 

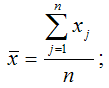
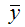
– среднее арифметическое значение переменной у:

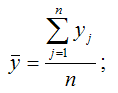
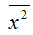
– среднее значение квадрата переменной х:

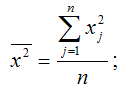
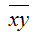
– среднее значение произведения переменных х и у:

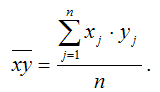
После того, как будут получены МНК-оценки неизвестных коэффициентов b0 и b1 линеаризованной двухфакторной производственной функции Кобба-Дугласа, на их основе можно будет рассчитать оценки неизвестных параметров A,a,? исходной функции Кобба-Дугласа.

Эффектом от масштаба производства для двухфакторной производственной функции называется изменение объёма произведённой продукции при пропорциональном изменении затрат труда и капитала.

Пусть объём основного капитала изменился на величину nK, а объём трудовых затрат увеличился на величину nL. Рассчитаем величину изменения объёма производства для функции двухфакторной производственной Кобба-Дугласа:

Q(n)=A*(nKa)*(nL?)= A*Ka*L?*na+?=Q*na+?.

Если справедливо неравенство (a+?)›1, то функция Кобба-Дугласа имеет возрастающий эффект от масштабов производства, т. е. с увеличением факторных переменных K и L в n раз, объём производства Q возрастает в na+? раз.

Если справедливо равенство (a+?)=1, то функция Кобба-Дугласа имеет фиксированный эффект от масштабов производства, т. е. с увеличением факторных переменных K и L в n раз, объём производства Q также возрастает в n раз.

Если справедливо неравенство (a+?)‹1, то функция Кобба-Дугласа имеет убывающий эффект от масштабов производства, т. е. с увеличением факторных переменных K и L в n раз, объём производства Q возрастает меньшими чем n темпами.