89. Условия идентификации структурной формы системы одновременных уравнений
89. Условия идентификации структурной формы системы одновременных уравнений
Введём следующие обозначения:
N – количество предопределённых переменных структурной формы системы одновременных уравнений;
n – количество предопределённых переменных в уравнении, проверяемом на идентифицируемость;
M – количество эндогенных переменных структурной формы системы одновременных уравнений;
m – количество эндогенных переменных в уравнении, проверяемом на идентифицируемость;
K – матрица коэффициентов при переменных, не входящих в уравнение, проверяемое на идентифицируемость.
Необходимые и достаточные условия идентификации применяются только к структурной форме системы одновременных уравнений.
Первое необходимое условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если оно исключает хотя бы N-1 предопределённую переменную:
(N–n)+(M–m)?N–1.
Второе необходимое условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если количество предопределённых переменных, не входящих в данное уравнение, будет не меньше числа эндогенных переменных этого уравнения минус единица:
N–n?m–1.
Достаточное условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если ранг матрицы K равен (N-1).
Рангом матрицы называется размер наибольшей её квадратной подматрицы, определитель которой не равен нулю.
На основе перечисленных условий идентификации, можно сформулировать необходимые и достаточные условия идентифицируемости уравнения структурной формы системы одновременных уравнений:
1) уравнение структурной формы системы одновременных уравнений считается сверхидентифицированным, если M–m>n–1 и ранг матрицы K равен (N-1);
2) уравнение структурной формы системы одновременных уравнений считается точно идентифицированным, если M–m=n–1 и ранг матрицы K равен (N-1);
3) уравнение структурной формы системы одновременных уравнений считается неидентифицированным, если M–m?n–1 и ранг матрицы K меньше (N-1);
4) уравнение структурной формы системы одновременных уравнений считается неидентифицированным, если M–m<n–1.
В качестве примера можно рассмотрим процесс идентификации структурной формы модели спроса и предложения. Данная модель включает в себя три уравнения:
1) уравнение предложения:
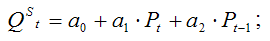
2) уравнение спроса:
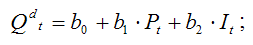
3) тождество равновесия:
QSt = Qdt
С учётом тождества равновесия, модель спроса-предложения может быть записана в виде:

Количество эндогенных переменных данной модели M равно двум (Pt и Qt), т.е. M=2. Количество предопределённых переменных данной модели N равно двум (Pt–1 и It), т.е. N=2.
Проверим выполнение первого необходимого условия идентифицируемости.
Для функции спроса выполняются равенства m=2 и n=1. Отсюда
(N–n)+(M–m)=(2–1)+(2–2)+(2–2)=1=(N–1)=1,
следовательно, уравнение спроса является точно идентифицированным.
Для функции предложения выполняются равенства m=2 и n=1. Отсюда
(N–n)+(M–m)=(2–1)+(2–2)+(2–2)=1=(N–1)=1,
следовательно, уравнение предложения является точно идентифицированным.
Проверим выполнение второго необходимого условия идентифицируемости.
Для функции спроса выполняются равенства m=2 и n=1. Отсюда
N–n=2–1=1=m–1=2–1=1,
следовательно, уравнение спроса является точно идентифицированным.
Для функции предложения выполняются равенства m=2 и n=1. Отсюда
N–n=2–1=1=m–1=2–1=1,
следовательно, уравнение предложения является точно идентифицированным.
Проверим выполнение достаточного условия идентифицируемости, заключающееся в том, чтобы хотя бы один из коэффициентов матрицы K не был равен нулю, т.к. M–1=1.
В первом уравнении модели исключена переменная It и матрица K=[b2]. Т.к. определитель данной матрицы не равен нулю, следовательно, rank=1=M–1 и уравнение является идентифицированным.
Во втором уравнении исключена переменная Pt–1 и матрица К=[a2]. Т.к. определитель данной матрицы не равен нулю, следовательно, rank=1=M–1 и уравнение является идентифицированным.
Т.к. уравнения спроса и предложения являются точно идентифицированными, то и система уравнений в целом точно идентифицирована.
Приведённая форма системы уравнений модели спроса-предложения:
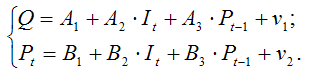
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
ИДЕНТИФИКАЦИИ КРИЗИС
ИДЕНТИФИКАЦИИ КРИЗИС социокультурный феномен, оформившийся в эпоху постмодерна (см.) и заключающийся в разрушении условий возможности целостного восприятии субъектом самого себя как самотожде- ственной личности. Авторство термина “И. К.” традиционно приписывается Дж.
27. УСЛОВИЯ ОПЛАТЫ ТРУДА. ФАКУЛЬТАТИВНЫЕ УСЛОВИЯ ТРУДОВОГО ДОГОВОРА
27. УСЛОВИЯ ОПЛАТЫ ТРУДА. ФАКУЛЬТАТИВНЫЕ УСЛОВИЯ ТРУДОВОГО ДОГОВОРА Один из главных вопросов, требующих отражения в трудовом договоре, – вопрос оплаты труда. Вопросы оплаты труда решаются непосредственно на предприятиях. Их регулирование осуществляется локальными
АНОМАЛИИ ПОЛОВОЙ ИДЕНТИФИКАЦИИ
АНОМАЛИИ ПОЛОВОЙ ИДЕНТИФИКАЦИИ ТРАНССЕКСУАЛИЗМТранссексуал убежден, что его истинный пол противоположен тому, на который указывают внешние половые признаки. Кроме того, он испытывает чувство отчужденности от собственного тела и непреодолимое желание вести образ
Расстройства половой идентификации
Расстройства половой идентификации ЖЕНОПОДОБНОЕ ПОВЕДЕНИЕ У МАЛЬЧИКОВНекоторые мальчики предпочитают одеваться в платья и охотнее играют с девочками, нежели с мальчиками. Многие из таких мальчиков и в поведении явно подражают девочкам и заявляют, что хотели бы быть
11. Условия оптимума для корпоративной системы России
11. Условия оптимума для корпоративной системы России Условия структурного оптимума для корпоративной системы примерно таковы же, какими они были в большинстве стран послевоенной Западной Европы, а также в Канаде и Австралии. Во-первых, это наличие крупного госсектора,
12. Условия оптимальности системы землепользования
12. Условия оптимальности системы землепользования Система землепользования должна быть построена исходя из той предпосылки, что земля является наиболее ценным из всех имеющихся активов. Не может игнорироваться и тот факт, что во время Второй мировой войны, защищая
15. Теория идентификации
15. Теория идентификации Основоположником практических методов идентификации был на заре криминалистики А. Бертильон. Но в основе теории идентификации лежат работы С. М. Потапова, не потерявшие своей актуальности по сей день.Понятие «идентификация» происходит от
16. Объекты криминалистической идентификации
16. Объекты криминалистической идентификации Объекты криминалистической идентификации делятся на идентифицируемые и идентифицирующие. К идентифицируемым объектам относятся те, в отношении которых решается вопрос о тождестве (оружие, применявшееся на месте
19. Виды и задачи криминалистической идентификации
19. Виды и задачи криминалистической идентификации Задача доказывания с использованием идентификации состоит в установлении единичного материального объекта и его связи с расследуемым событием. Так вот, единичный объект, установленный путем идентификации, только
87. Системы эконометрических уравнений
87. Системы эконометрических уравнений Если экономический процесс не поддаётся описанию посредством одной модели регрессии, то в подобных ситуациях прибегают к построению нескольких эконометрических уравнений, которые в совокупности образуют систему.В состав системы
88. Структурная и приведённая формы системы одновременных уравнений. Идентификация модели
88. Структурная и приведённая формы системы одновременных уравнений. Идентификация модели Структурными уравнениями называются уравнения, из которых состоит исходная система одновременных уравнений. В данном случае система имеет структурную форму.Структурная форма
93. Спецификация и приведенная форма эконометрических моделей в виде системы одновременных уравнений. Эконометрическая модель Самуэльсона-Хикса делового цикла экономики
93. Спецификация и приведенная форма эконометрических моделей в виде системы одновременных уравнений. Эконометрическая модель Самуэльсона-Хикса делового цикла экономики Определение явного вида эконометрической модели называется спецификацией эконометрической