88. Структурная и приведённая формы системы одновременных уравнений. Идентификация модели

88. Структурная и приведённая формы системы одновременных уравнений. Идентификация модели

Структурными уравнениями называются уравнения, из которых состоит исходная система одновременных уравнений. В данном случае система имеет структурную форму.

Структурная форма системы одновременных уравнений непосредственно характеризует реальный экономический процесс.

Структурными коэффициентами или параметрами называются коэффициенты уравнений структурной формы системы одновременных уравнений.

Структурные уравнения могут быть представлены либо поведенческими уравнениями, либо уравнениями-тождествами.

Поведенческие уравнения характеризуют все типы взаимодействия между эндогенными и экзогенными переменными в структурной форме системы одновременных уравнений.

В поведенческих уравнениях значения параметров являются неизвестными и подлежат оцениванию.

Примером поведенческого уравнения являются уравнение спроса или уравнение предложения в модели спроса-предложения:

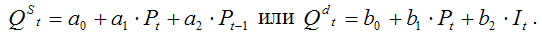
Тождествами называют равенства, которые выполняются во всех случаях.

Отличительной чертой тождеств является то, что их вид и значения параметров известны, и они не содержат случайной компоненты.

Примером уравнения-тождества является тождество равновесия в модели спроса-предложения:

QSt = Qdt

Для того чтобы определить неизвестные структурные коэффициенты системы одновременных уравнений необходимо перейти к приведённой форме системы.

Приведённой формой системы одновременных уравнений называется система независимых уравнений, в которой все эндогенные переменные выражены только через экзогенные или предопределённые переменные и случайные компоненты, например:

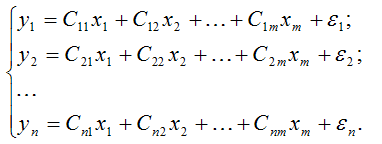
Приведёнными коэффициентами или параметрам называются коэффициенты приведённой формы системы одновременных уравнений.

Оценки неизвестных приведённых коэффициентов можно рассчитать с помощью классического метода наименьших квадратов, а уже на их основе определить оценки структурных коэффициентов.

При переходе от структурной формы системы одновременных уравнений к приведённой форме может возникнуть проблема идентификации модели.

Проблема идентификации состоит в возможности численной оценки неизвестных коэффициентов структурных уравнений по МНК-оценкам коэффициентов приведённых уравнений.

Исходная система одновременных уравнений называется идентифицированной, если все её уравнения точно идентифицированы.

Уравнение называется точно идентифицированным, если по оценкам коэффициентов приведённой формы системы одновременных уравнений можно однозначно найти оценки коэффициентов структурной формы системы одновременных уравнений.

Признаком идентифицированности системы одновременных уравнений является равенство между количеством уравнений, определяющих структурные коэффициенты, и количеством этих коэффициентов, т. е. квадратная форма структурной системы уравнений.

Исходная система одновременных уравнений называется сверхидентифицированной, если среди уравнений модели есть хотя бы одно сверхидентифицированное.

Уравнение называется сверхидентифицированным, если по оценкам коэффициентов приведённой формы системы одновременных уравнений можно получить более одного значения для коэффициентов структурной формы системы одновременных уравнений.

Исходная система одновременных уравнений называется неидентифицированной, если среди уравнений системы есть хотя бы одно неидентифицированное.

Уравнение называется неидентифицированным, если по оценкам коэффициентов приведённой формы системы одновременных уравнений невозможно рассчитать оценки коэффициентов структурной формы системы одновременных уравнений.

Данный текст является ознакомительным фрагментом.