45. Показатели корреляции и детерминации для нелинейных моделей регрессии

45. Показатели корреляции и детерминации для нелинейных моделей регрессии

Индексом корреляции для нелинейных форм связи называется коэффициент корреляции, который вычисляется для оценки качества построенной нелинейной модели регрессии.

Индекс корреляции для нелинейных форм вычисляется с помощью теоремы о разложении дисперсий по формуле:

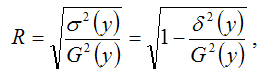
где G2(y) – это общая дисперсия зависимой переменной;

?2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:

?2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:

Также индекс корреляции для нелинейных форм можно рассчитать с помощью теоремы о разложении сумм квадратов по формуле:

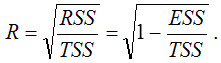
где RSS (Regression Sum Square) – сумма квадратов объяснённой регрессии:

ESS (Error Sum Square) – сумма квадратов остатков модели множественной регрессии с n независимыми переменными:

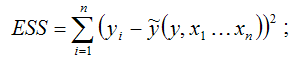
TSS (TotalSumSquare) – общая сумма квадратов модели множественной регрессии с n независимыми переменными:

Индекс корреляции для нелинейных форм связи изменяется в пределах от нуля до единицы. С его помощью нельзя охарактеризовать направление связи между результативной и факторными переменными. Чем ближе значение индекса корреляции для нелинейных форм связи к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение индекса корреляции для нелинейных форм связи к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.

Индексом детерминации называется квадрат индекса корреляции для нелинейных форм связи.

Расчёт индекса детерминации с помощью теоремы о разложении дисперсий:

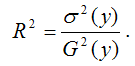
Расчёт индекса детерминации с помощью теоремы о разложении сумм квадратов:

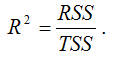
Индекс детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.

Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.

Данный текст является ознакомительным фрагментом.