30. Частные коэффициенты корреляции для линейной модели регрессии с двумя факторными переменными

30. Частные коэффициенты корреляции для линейной модели регрессии с двумя факторными переменными

Частные коэффициенты корреляции используются для оценки зависимости между результативной переменной и одной из факторных переменных при условии постоянства всех остальных факторных переменных, включённых в модель множественной регрессии. Таким образом, частный коэффициент корреляции позволяет элиминировать влияние на результат всех факторных модельных переменных кроме одной.

Рассчитаем частные коэффициенты корреляции на основе линейной модели регрессии с двумя факторными переменными.

Общий вид модели двухфакторной регрессии:

yi=?0+?1xi+?2zi+?i,

где yi – результативная переменная,

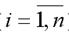
xi – первая факторная переменная;

zi – второй факторная переменная;

?0, ?1, ?2– неизвестные коэффициенты модели регрессии;

?i – случайная ошибка модели регрессии.

Для определения степени зависимости между результативной переменной yiи факторной переменной xi при постоянном значении факторной переменой zi и результативной переменной yi и факторной переменной zi при постоянном значении факторной переменной xi используются частные коэффициенты корреляции первого порядка, потому что они позволяют элиминировать влияние только одного признака. Порядок частного коэффициента корреляции характеризуется количеством признаков, влияние которых устраняется. Для модели парной регрессии рассчитывается коэффициент корреляции нулевого порядка.

Коэффициент частной корреляции между результативной переменной yi и факторной переменной xiпри постоянном значении факторной переменой ziрассчитывается по формуле:

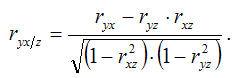
Коэффициент частной корреляции между результативной переменной yi и факторной переменной ziпри постоянном значении факторной переменной xi рассчитывается по формуле:

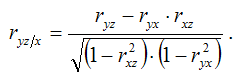
Кроме влияния на результативную переменную, частный коэффициент корреляции позволяет рассчитать степень зависимости между факторными переменными.

Коэффициент частной корреляции между факторной переменной xi и факторной переменной ziпри постоянном значении результативной переменной yi рассчитывается по формуле:

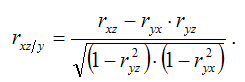
Рассмотренные коэффициенты частной корреляции изменяются в пределах от минус единицы до единицы.

Частные коэффициенты корреляции также можно рассчитать через коэффициент множественной детерминации.

Коэффициент частной корреляции между результативной переменной yi и факторной переменной xi при постоянном значении факторной переменой zi:

где

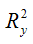
– множественный коэффициент детерминации двухфакторной модели регрессии.

Данный коэффициент корреляции изменяется в пределах от нуля до единицы.

При проверке значимости частных коэффициентов корреляции выдвигается основная гипотеза о незначимости данных коэффициентов, например:

Н0:ryx/z=0.

Тогда конкурирующей или альтернативной гипотезой будет гипотеза вида:

Н1:ryx/z?0.

Проверка выдвинутых гипотез осуществляется с помощью t-критерия Стьюдента.  Критическое значение t-критерия tкрит(а,n-h) определяется по таблице распределения Стьюдента, где а – уровень значимости, (n-h) – число степеней свободы. Для модели двухфакторной регрессии число степеней свободы равно (n-3).

Наблюдаемое значение t-критерия рассчитывается по формуле (на примере частного коэффициента корреляции между результативной переменной yi и факторной переменной xi при постоянном значении факторной переменой zi):

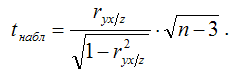
Если |tнабл|?tкрит, то основная гипотеза не отклоняется, и частный коэффициент корреляции является незначимым. Следовательно, между переменными х и у при постоянном значении переменой z корреляционная связь отсутствует.

Если |tнабл|>tкрит,  то основная гипотеза отклоняется в пользу конкурирующей гипотезы с вероятностью совершения ошибки первого рода а. В этом случае можно считать, что между переменными х и у при постоянном значении переменной z существует корреляционная зависимость.

Частные коэффициенты корреляции позволяют сделать вывод об обоснованности включения переменной в модель регрессии. Если значение частного коэффициента корреляции мало или коэффициент незначим, то связь между данной факторной переменной и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели без ущерба для её качества.

Данный текст является ознакомительным фрагментом.