33. Коэффициент множественной корреляции. Коэффициент множественной детерминации

33. Коэффициент множественной корреляции. Коэффициент множественной детерминации

Если частные коэффициенты корреляции модели множественной регрессии оказались значимыми, т. е. между результативной переменной и факторными модельными переменными действительно существует корреляционная взаимосвязь, то в этом случае построение множественного коэффициента корреляции считается целесообразным.

С помощью множественного коэффициента корреляции характеризуется совокупное влияние всех факторных переменных на результативную переменную в модели множественной регрессии.

Коэффициент множественной корреляции для линейной модели множественной регрессии с n факторными переменными рассчитывается через стандартизированные частные коэффициенты регрессии и парные коэффициенты корреляции по формуле:

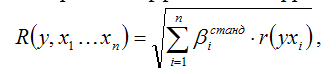
где r (yxi) – парный (не частный) коэффициент корреляции между результативной переменной у и факторной переменной xi

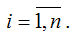
Коэффициент множественной корреляции изменяется в пределах от нуля до единицы. С его помощью нельзя охарактеризовать направление связи между результативной и факторными переменными. Чем ближе значение множественного коэффициента корреляции к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение множественного коэффициента корреляции к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.

Коэффициентом множественной детерминации R2 называется квадрат множественного коэффициента корреляции:

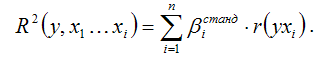
Коэффициент множественной детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.

Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.

Для коэффициента множественной детерминации всегда выполняется неравенство вида:

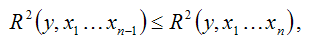
Следовательно, включение в линейную модель регрессии дополнительной факторной переменной xn не снижает значения коэффициента множественной детерминации.

Коэффициент множественной детерминации может быть определён не только как квадрат множественного коэффициента корреляции, но и с помощью теоремы о разложении сумм квадратов по формуле:

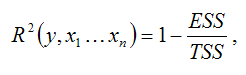
где ESS (Error Sum Square) – сумма квадратов остатков модели множественной регрессии с n независимыми переменными:

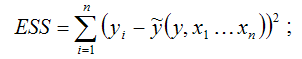
TSS (TotalSumSquare) – общая сумма квадратов модели множественной регрессии с n независимыми переменными:

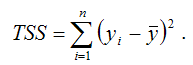
Однако классический коэффициент множественной детерминации не всегда способен определить влияние на качество модели регрессии дополнительной факторной переменной. Поэтому наряду с обычным коэффициентом рассчитывают также и скорректированный (adjusted) коэффициент множественной детерминации, в котором учитывается количество факторных переменных, включённых в модель регрессии:

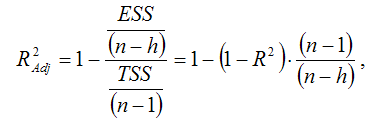
где n – количество наблюдений в выборочной совокупности;

h – число параметров, включённых в модель регрессии.

При большом объёме выборочной совокупности значения обычного и скорректированного коэффициентов множественной детерминации отличаться практически не будут.