26. Линейная модель множественной регрессии
26. Линейная модель множественной регрессии
Построение модели множественной регрессии является одним из методов характеристики аналитической формы связи между зависимой (результативной) переменной и несколькими независимыми (факторными) переменными.
Модель множественной регрессии строится в том случае, если коэффициент множественной корреляции показал наличие связи между исследуемыми переменными.
Общий вид линейной модели множественной регрессии:
yi=?0+?1x1i+…+?mxmi+?i,
где yi – значение i-ой результативной переменной,
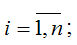
x1i…xmi – значения факторных переменных;
?0…?m – неизвестные коэффициенты модели множественной регрессии;
?i – случайные ошибки модели множественной регрессии.
При построении нормальной линейной модели множественной регрессии учитываются пять условий:
1) факторные переменные x1i…xmi – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии ?i;
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
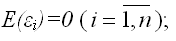
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
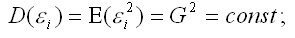
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т.е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
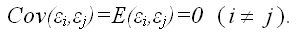
Это условие выполняется в том случае, если исходные данные не являются временными рядами;
5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: ?i~N(0, G2).
Общий вид нормальной линейной модели парной регрессии в матричной форме:
Y=X* ?+?,
Где
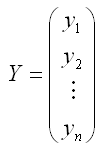
– случайный вектор-столбец значений результативной переменной размерности (n*1);
– матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент ?0 умножается на единицу;
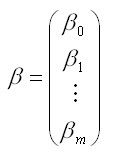
– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);
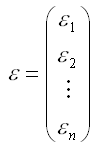
– случайный вектор-столбец ошибок модели регрессии размерности (n*1).
Включение в линейную модель множественной регрессии случайного вектора-столбца ошибок модели обусловлено тем, что практически невозможно оценить связь между переменными со 100-процентной точностью.
Условия построения нормальной линейной модели множественной регрессии, записанные в матричной форме:
1) факторные переменные x1j…xmj – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии ?i. В терминах матричной записи Х называется детерминированной матрицей ранга (k+1), т.е. столбцы матрицы X линейно независимы между собой и ранг матрицы Х равен m+1<n;
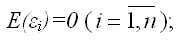
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
3) предположения о том, что дисперсия случайной ошибки модели регрессии является постоянной для всех наблюдений и ковариация случайных ошибок любых двух разных наблюдений равна нулю, записываются с помощью ковариационной матрицы случайных ошибок нормальной линейной модели множественной регрессии:
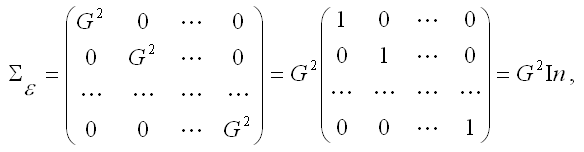
где
G2 – дисперсия случайной ошибки модели регрессии ?;
In – единичная матрица размерности (n*n).
4) случайная ошибка модели регрессии ? является независимой и независящей от матрицы Х случайной величиной, подчиняющейся многомерному нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: ??N(0;G2In.
В нормальную линейную модель множественной регрессии должны входить факторные переменные, удовлетворяющие следующим условиям:
1) данные переменные должны быть количественно измеримыми;
2) каждая факторная переменная должна достаточно тесно коррелировать с результативной переменной;
3) факторные переменные не должны сильно коррелировать друг с другом или находиться в строгой функциональной зависимости.
Данный текст является ознакомительным фрагментом.