9. Общая модель парной (однофакторной) регрессии
9. Общая модель парной (однофакторной) регрессии
Общая модель парной регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений.
Регрессионным анализом называется определение аналитического выражения связи между исследуемыми переменными, в котором изменение результативной переменной происходит под влиянием факторной переменной.
Модель регрессии или уравнение регрессии позволяет количественно оценить взаимосвязь между исследуемыми переменными.
Предположим, что имеется набор значений двух переменных: yi (результативная переменная) и xi (факторная переменная). Между этими переменными существует зависимость вида: y = f (x).
Задача регрессионного анализа состоит в том, чтобы по данным наблюдений определить такую функцию ? = f (x), которая наилучшим образом описывала исследуемую зависимость между переменными.
Для определения аналитической формы зависимости между исследуемыми переменными применяются следующие методы:
1) графический метод или визуальная оценка характера связи. В этом случае на линейном графике по оси абсцисс откладываются значения факторной переменной х, а по оси ординат – значения результативной переменной у. Затем на пересечении соответствующих значений отмечаются точки. Полученный точечный график в системе координат (х, у) называется корреляционным полем. Линия, которая соединяет точки на графике, называется эмпирической линией. По её виду можно судить не только о наличии, но и о форме зависимости между изучаемыми переменными;
2) на основе теоретического и логического анализа природы изучаемых явлений, их социально-экономической сущности;
3) определение аналитической формы зависимости между переменными экспериментальным путём.
При исследовании зависимости между двумя переменными чаще всего используется линейная форма связи. Это связано с двумя обстоятельствами:
1) чёткая экономическая интерпретация параметров линейной модели регрессии;
2) в большинстве случаев нелинейные модели регрессии преобразуются к линейному виду.
Общий вид модели парной регрессии зависимости переменной у от переменной х:
yi=?0+?1xi+?i,
где yi– результативные переменные,
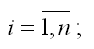
xi– факторные переменные,
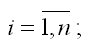
?0, ?1 – параметры модели регрессии, подлежащие оцениванию;
?i – случайная ошибка модели регрессии. Данная величина является случайной, она характеризует отклонения реальных значений результативных переменных от теоретических, рассчитанных по уравнению регрессии.
Присутствие случайной ошибки в модели регрессии порождено следующими источниками:
1) нерепрезентативность выборки. Модель парной регрессии в большинстве случаев является большим упрощением истинной зависимости между переменными, потому что в модель входит только одна факторная переменная, не способная полностью объяснить вариацию результативной переменной. При этом результативная переменная может быть подвержена влиянию множества других факторных переменных в гораздо большей степени;
2) ошибки, возникающие при измерении данных;
3) неправильная функциональная спецификация модели.
Коэффициент ?1, входящий в модельпарной регрессии, называется коэффициентом регрессии. Он характеризует, на сколько в среднем изменится результативная переменная у при условии изменения факторной переменной х на единицу своего измерения. Знак коэффициента регрессии указывает на направление связи между переменными:
1) если ?1›0, то связь между изучаемыми переменными (с уменьшением факторной переменной х уменьшается и результативная переменная у, и наоборот);
2) если ?1‹0, то связь между изучаемыми переменными (с увеличением факторной переменной х результативная переменная у уменьшается, и наоборот).
Коэффициент ?0, входящий в модель парной регрессии, трактуется как среднее значение результативной переменной у при условии, что факторная переменная х равна нулю. Но если факторная переменная не имеет и не может иметь нулевого значения, то подобная трактовка коэффициента ?0 не имеет смысла.
Общий вид модели парной регрессии в матричном виде:
Y= X* ?+ ?,
где
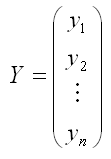
– случайный вектор-столбец значений результативной переменной размерности n x 1;
– матрица значений факторной переменной размерности n x 2. Первый столбец является единичным, потому что в модели регрессии коэффициент ?0 умножается на единицу;
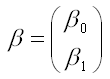
– вектор-столбец неизвестных коэффициентов модели регрессии размерности 2 x 1;
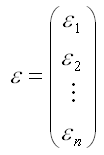
– случайный вектор-столбец ошибок модели регрессии размерности n x 1.
Данный текст является ознакомительным фрагментом.