Гидродинамический метод прогноза

Гидродинамический метод прогноза

Данные измерений уровня воды в Балтийском море и Финском заливе показывают, что наводнения представляют собой волны, горизонтальные размеры которых значительно превосходят глубину бассейна. Эта особенность наводнений позволяет применить к их изучению один из самых развитых разделов гидродинамики – теорию «длиных волн на мелкой воде». Фундаментальная формула этой теории для скорости волны, зависящая только от глубины водоема (учитывается также постоянная величина – ускорение свободного падения), приводит к значениям, очень близким к эмпирическим, получаемым из наблюдений.

Основы теории «длинных волн» разработаны трудами великих ученых – И. Ньютона, Д. Бернулли, Л. Эйлера, Ж. Лагранжа, П.-С. Лапласа. С ее помощью более двух веков назад получены замечательные результаты в исследовании морских приливов, включая необходимое для практики их предвычисление. С 1950-х гг. приложения теории «длинных волн на мелкой воде» распространились на изучение морских наводнений, сейшей, приливов, речных половодий и паводков. В начале 1960-х гг. ее применили к прогнозу наводнений в Ленинграде.^[98]

Популярное изложение математической теории – занятие неблагодарное и, строго говоря, невозможное. Нельзя в полной мере сочетать научную строгость, воплощенную в математической теории, с доступностью популярного изложения. Нельзя исчерпывающе объяснить математическую задачу простым языком, но передать общий смысл в какой-то степени можно, что мы и попытаемся исполнить ниже. Однако необходимо помнить, что у математики свой язык, совершенно отвлеченный, не похожий ни на какой другой. На этом языке люди научились кратко и содержательно излагать характер окружающих нас природных явлений. С помощью математического языка решаются конкретные научные и технические задачи, для которых известны исходные положения и поставлены конечные цели.

Инженеры-практики, и синоптики в том числе, пользуются расчетными формулами, соотношениями, зависимостями, в самом общем виде представляя себе, что весь их рабочий аппарат основан на небольшом числе фундаментальных теорий и уравнений математической физики, статистической термодинамики, гидро– и аэромеханики. В нашем случае гидродинамическая теория «длинных волн на мелкой воде», выраженная математическим языком в виде уравнений, позволяет преобразовать определенный набор исходной информации в интересующий нас прогностический результат. Попытаемся популярно изложить эту процедуру, опуская математическую постановку задачи и способы ее решения.

Теория «длинных волн на мелкой воде» математически описывается системой дифференциальных уравнений в частных производных. Этих уравнений три: два уравнения движения и одно – неразрывности. Уравнения выражают основные законы физики: второй закон Ньютона и закон сохранения массы. В уравнениях содержатся все физические характеристики, с которыми связаны наводнения: время, расстояния, глубины, географическая широта, ускорение свободного падения, угловая скорость вращения Земли, коэффициенты трения воды о дно и воздуха о поверхность воды. Уравнения требуют задания действующих сил – ветра и атмосферного давления, а также начального состояния движения и условий на границах бассейна.

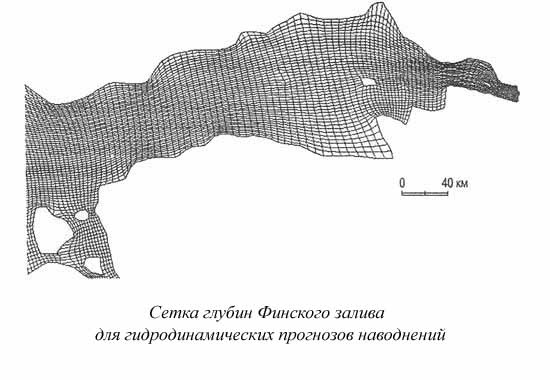
Решить такую систему уравнений и рассчитать реальный подъем воды в конкретном объекте можно только специальными методами и, конечно, с помощью компьютера. Вычисления выполняются шагами по времени и пространству на сетке, которой покрывается изучаемый объект, в нашем случае – Трансбалтика, Финский залив или вся акватория Балтийского моря.

Объем вычислений огромен. В начале 1960-х гг. одна из первых отечественных электронных вычислительных машин-«Урал-1» – выполняла гидродинамический прогноз, причем на грубой сетке, со скоростью самого подъема воды, так сказать, в режиме реального времени, что совершенно непригодно для заблаговременного прогноза. Но техника развивалась быстро, и в 1967 г. уже был составлен первый прогноз реального наводнения в Ленинграде. На современных компьютерах гидродинамические прогнозы составляются при каждой угрозе наводнений за считанные минуты. Да еще в нескольких вариантах (скажем, с различными вариантами метеорологических прогнозов). Полученные результаты оцениваются, причем также математически, непременно сопоставляются с показателями, выведенными эмпирическим методом, после чего принимается прогностическое решение. Неудачный прогноз, конечно, уже ничто спасти не может, но поиски причин неудачи продолжаются и после наводнения. Вся эта исследовательская интересная, но во многом и рутинная утомительная работа весьма схожа с работой в физической (химической, биологической) лаборатории. Она и получила название «численный эксперимент».^[99]

Гидродинамический метод расчета и прогноза наводнений является наиболее общим и универсальным. Он использует всю доступную информацию и описывает явление полностью во времени и по всему морю (можно было бы привести результаты для Кронштадта, Гогланда, Таллинна…). Но его недостаток – в невозможности корректуры в течение по крайней мере трех– шести часов до поступления нового прогноза атмосферного давления, скорости и направления ветра. Так организована служба регулярных прогнозов. За это время прогноз наводнения может оказаться запоздалым. Синоптики же способны вводить информацию с отдельных станций даже ежечасно. Гидродинамический метод гораздо более склонен к совершенствованию с помощью численных экспериментов. Эмпирический же ограничен рамками заданной формулы, хотя и привлекательно простой. Его возможности к уточнению и повышению качества практически исчерпаны. Правда, формулы прогноза уровня воды в Петербурге можно составить не только по показаниям в Таллинне, но и с использованием данных любого пункта Трансбалтики, где производятся измерения уровня воды и силы ветра. Тогда образуется система уравнений, мало уступающая по объему гидродинамической, и эмпирический метод утратит простоту и быстроту.

Принципиально же методы не противоречат друг другу. Тот и другой учитывают волновую природу наводнений, их метеорологическое происхождение и влияние атмосферных факторов. Их противопоставление, продолжавшееся около тридцати лет, было вызвано вовсе не научными или техническими причинами. Теперь есть все возможности взаимодействия двух методов и, соответственно, улучшения качества прогнозов наводнений в Петербурге.

Применение гидродинамической модели к прогнозу далеко не единственное ее приложение. С ее помощью проводились все расчеты для проекта защитных сооружений. Быстро и дешево были получены результаты влияния дамбы на подъемы воды различной высоты, на скорости течений, на распределение потоков. Воспроизводились еще не наблюдавшиеся ранее наводнения редкой повторяемости. Модель дополнялась другими уравнениями, что позволило оценить экологическое влияние защитных сооружений. И сейчас, когда строительство, хотя и медленно, продолжается, возникают новые вопросы, за ответом на которые обращаются прежде всего к гидродинамической модели наводнений.

Данный текст является ознакомительным фрагментом.