15. Оценка дисперсии случайной ошибки модели регрессии
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
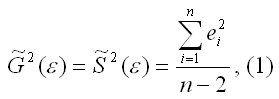
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
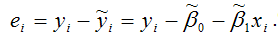
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
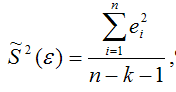
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
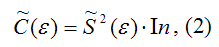
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
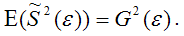
Доказательство. Примем без доказательства справедливость следующих равенств:
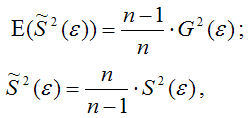
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
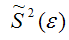
– выборочная оценка дисперсии случайной ошибки.
Тогда:
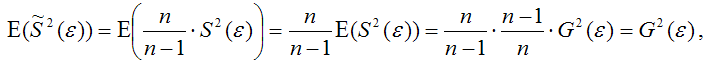
т. е.
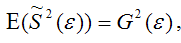
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
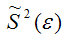
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
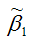
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
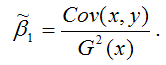
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
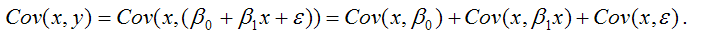
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
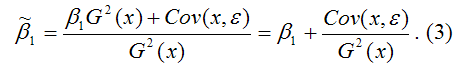
Таким образом, МНК-оценка
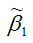
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
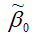
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
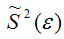
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.