44. Методы нелинейного оценивания коэффициентов модели регрессии

44. Методы нелинейного оценивания коэффициентов модели регрессии

Функцией потерь или ошибок называется функционал вида

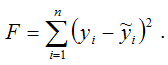
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических значений ?:

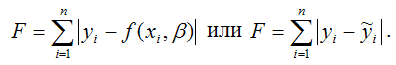
Функция потерь характеризует потери в точности аппроксимации исходных данных построенной моделью регрессии.

В интересах исследователя минимизировать функцию ошибок. Для этого используются различные методы, однако, их общий недостаток заключается в наличии локальных минимумов. Например, если оценка неизвестного параметра модели регрессии будет немного изменена, то значение функция потерь практически не изменится, но существует вероятность того, что ошибочное значение оцениваемого параметра модели регрессии даст в результате ощутимое уменьшение функции ошибок. Такое явление называется локальным минимумом.

Следствием локальных минимумов являются неоправданно завышенные или заниженные оценки неизвестных параметров модели регрессии.

Избежать попадания в локальный минимум можно путём повторения процедуры оценивания неизвестных параметров модели регрессии с изменёнными начальными условиями (шагом, ограничением оцениваемых параметров и т. д.).

При достижении функцией ошибок глобального минимума, оценки неизвестных коэффициентов модели регрессии считаются оптимальными.

К основным методам минимизации функции ошибок относятся:

1) метод Ньютона. В соответствии с данным методом основной шаг в направлении глобального минимума метода Ньютона рассчитывается по формуле:

где ?k– вектор значений оцениваемых параметров на k-ой итерации;

Н – матрица вторых частных производных, или матрица Гессе;

gk – вектор градиента на k-ой итерации.

Предположим, что задана скалярная функция у от переменных

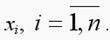
вида y=f(x).

Независимые переменные xi можно записать в виде вектора: x=[x1x2…xn]T. Тогда по определению производной:

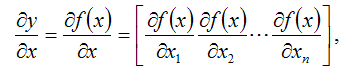
Вектор-столбец

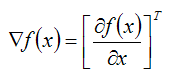
называется градиентом функции y=f(x) в точке x;

2) для избежания громоздких вычислений матрицы Гессе существуют различные способы её замены приближёнными выражениями. Эти приёмы легли в основу квазиньютоновых методов. Суть квазиньютоновых методов заключается в том, что в различных точках вычисляются значения функции ошибок для определения первой и второй производной. Первая производная функции в заданной точке равна тангенсу угла наклона графика функции, а вторая производная функции в заданной точке равна скорости его изменения. Затем эти данные применяются для определения направления изменения параметров, а соответственно, и для минимизации функции ошибок;

3) симплекс-метод – это метод нелинейного оценивания, который не использует производные функции ошибок. При каждой итерации функция ошибок оценивается в n+1 точках n-мерного пространства, образуя при этом фигуру, называемую симплексом. В многомерном пространстве симплекс будет постепенно менять параметры, смещаясь в сторону минимизации функции потерь. Основное преимущество симплекс-метода перед остальными методами нелинейного оценивания заключается в том, что при слишком большом шаге для точного определения направления минимизации функции потерь или при слишком большом симплексе, алгоритм автоматически уменьшает симплекс, и вычислительная процедура продолжается. При обнаружении минимума, симплекс вновь увеличивается для проверки минимума на локальность.