47. Тесты Бокса-Кокса и Зарембеки выбора модели регрессии

47. Тесты Бокса-Кокса и Зарембеки выбора модели регрессии

Если в начале эконометрического моделирования перед исследователем стоит выбор между моделью регрессии, внутренне нелинейной и линейной моделью регрессии (или сводящейся к линейному виду), то предпочтение отдаётся линейным формам моделей.

Однако многие модели регрессии различной функциональной формы нельзя сравнивать с помощью стандартных критериев (например, сравнение по множественному коэффициенту детерминации, или суммам квадратов отклонений), которые позволили бы подобрать наиболее подходящую модель регрессии.

Например, если перед исследователем стоит вопрос о выборе линейной или логарифмической моделями регрессии, то использовать при этом критерий суммы квадратов отклонений нельзя, потому что общая сумма квадратов отклонений для логарифмической модели намного меньше, чем для линейной модели регрессии. Это вызвано тем, что значение логарифма результативной переменной logy намного меньше, чем соответствующее значение у, поэтому сравнение сумм квадратов отклонений моделей даёт неадекватные результаты.

Если сравнивать данные модели по критерию коэффициента множественной детерминации, то мы вновь получим неадекватные результаты. Коэффициент множественной детерминации для линейной модели регрессии характеризует объяснённую регрессией долю дисперсии результативной переменной у. Индекс детерминации для логарифмической модели регрессии характеризует объяснённую регрессией долю дисперсии переменной logy. Если значения данных критериев примерно равны, то сделать выбор между моделями регрессии с их помощью также не представляется возможным.

Одним из методов проверки предположения о возможной линейной зависимости между исследуемыми переменными является метод проверки гипотезы о линейной зависимости между переменными с помощью коэффициента детерминации r2 и индекса детерминации R2.

Другим методом выбора функциональной зависимости между переменными является тест Бокса-Кокса.

Предположим, что перед исследователем стоит задача выбора между линейной и логарифмической моделями регрессии. Рассмотрим применение теста Бокса-Кокса на данном примере.

Тест Бокса-Кокса основывается на утверждении о том, что (у-1) и logy являются частными случаями функции вида

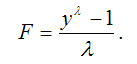
В том случае, если параметр ? равен единице, то данная функция принимает вид F=y-1.

В том случае, если параметр ? стремиться к нулю, то данная функция принимает вид F=logy.

Для того чтобы определить оптимальное значение параметра ?, необходимо провести несколько серий экспериментов с множеством значений данного параметра. С помощью такого перебора можно рассчитать такое значение параметра ?, которое даст минимальную величину критерия суммы квадратов отклонений. Подобный метод вычисления оптимального значения параметра называется поиском на решётке или на сетке значений.

П. Зарембеки разработал один из вариантов теста Бокса-Кокса специально для случая выбора между линейной и логарифмической моделями регрессии.

Суть данного теста заключается в том, что к результативной переменной у применяется процедура масштабирования. Подобное преобразование в дальнейшем позволит сравнивать величины сумм квадратов отклонений линейной и логарифмический моделей регрессий.

Тест Зарембеки реализуется в несколько шагов:

1) рассчитывается среднее геометрическое значений результативной переменной у по формуле:

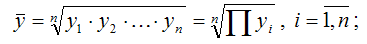
2) все результативные переменные у масштабируются по формуле:

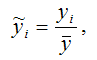
где ?i – масштабированное значение результативной переменной у для i-го наблюдения;

3) оценивается линейная модель регрессии с использованием масштабированных значений ?i результативной переменной вместо у, и логарифмическая модель регрессии с использованием ?i вместо logy. Все факторные переменные и коэффициенты регрессии остаются при этом неизменными. После такого масштабирования результативных переменных значения сумм квадратов отклонений для данных моделей регрессии можно сравнивать между собой. Поэтому выбирается та модель регрессии, для которой данный критерий окажется наименьшим.