56. Метод максимума правдоподобия

56. Метод максимума правдоподобия

Метод максимума правдоподобия (maximum likelihood function) применяется для определения неизвестных коэффициентов модели регрессии и является альтернативой методу наименьших квадратов. Суть данного метода состоит в максимизации функции правдоподобия или её логарифма.

Общий вид функции правдоподобия:

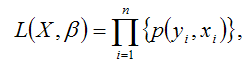
где

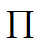
– это геометрическая сумма, означающая перемножение вероятностей по всем возможным случаям внутри скобок.

Предположим, что на основании полученных данных была построена модель регрессии бинарного выбора, где результативная переменная представлена с помощью латентной переменной:

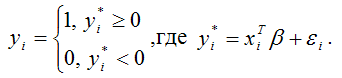
Следовательно, вероятность события, что результативная переменная yi примет значение, равное единице, можно выразить следующим образом:

Вероятность события, что результативная переменная yi примет значение, равное нулю, можно выразить следующим образом:

В связи с тем, что для вероятностей считается справедливым равенство вида:

функция правдоподобия может быть записана как геометрическая сумма вероятностей наблюдений:

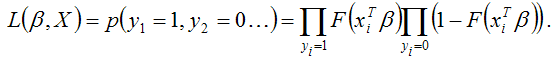
Для логит-регрессии и пробит-регрессии функция правдоподобия строится через сумму натуральных логарифмов правдоподобия следующим образом:

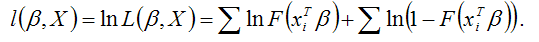
Оценки неизвестных параметров логит-регрессии и пробит-регрессии определяются с помощью максимизации функции правдоподобия:

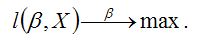
Для определения максимума функции l(?,X) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений:

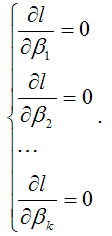
С помощью преобразований данной системы уравнений переходим к системе нормальных уравнений, решениями которой и будут оценки максимального правдоподобия

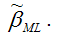
Прежде, чем использовать пробит-регрессию и логит-регрессию для прогнозирования или анализа, необходимо проверить значимость вычисленных коэффициентов пробит и логит регрессий и моделей регрессии в целом. Подобная проверка осуществляется с помощью величины (l1-l0), где параметр l1 соответствует максимально правдоподобной оценке основной модели регрессии, а параметр l0 – оценка нулевой модели регрессии, т. е. yi=?0.

При проверке значимости коэффициентов пробит или логит-регрессии выдвигается основная гипотеза о незначимости данных коэффициентов:

H0:?1=?2=…=?k=0.

Тогда конкурирующей или альтернативной гипотезой будет гипотеза вида:

H1:?1??2?…??k?0.

Для проверки выдвинутых гипотез рассчитывается величина H=-2(l1–l0), которая распределена по ?2закону распределения с k степенями свободы.

Критическое значение ?2-критерия определяется по таблице по ?2распределения в зависимости от заданного значения вероятности а и степени свободы k.

При проверке гипотез возможны следующие ситуации:

Если величина H больше критического значение ?2-критерия, т.е.

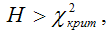
то основная гипотеза отвергается, и коэффициенты модели регрессии являются значимыми. Следовательно, модель пробит или логит-регрессии также является значимой.

Если величина H меньше критического значение ?2-критерия, т. е.

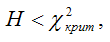
то основная гипотеза принимается, и коэффициенты модели регрессии являются незначимыми. Следовательно, модель пробит или логит-регрессии также является незначимой.

Оценки неизвестных коэффициентов модели регрессии, полученные методом максимума правдоподобия, удовлетворяют следующему утверждению.

Пусть ? – это элемент, принадлежащий заданному пространству А. Если А является открытым интервалом, а функция L(?) дифференцируема и достигает максимума в заданном интервале A, то оценки максимального правдоподобия удовлетворяют равенству вида:

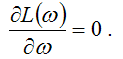
Докажем данное утверждение на примере модели логит-регрессии.

Функция максимального правдоподобия для модели логит-регрессии имеет вид:

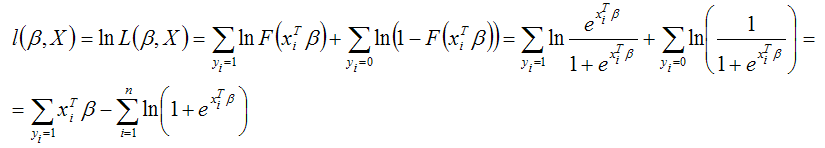
Продифференцируем полученную функцию по параметру ?:

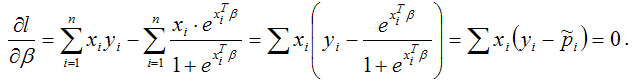
Следовательно, утверждение можно считать доказанным.

В том случае, если для модели регрессии справедливы предпосылки нормальной линейной модели регрессии, то оценки неизвестных коэффициентов, полученные с помощью метода наименьших квадратов, и оценки, полученные с помощью метода максимума правдоподобия, будут совпадать.