§ 5 Рождение науки

Аристотель научил меня удовлетворять свой разум только тем, в чём убеждают меня рассуждения, а не только авторитет учителя…

Г. Галилей

Отсюда станет понятным на бесчисленных примерах, сколь полезна математика в заключениях, касающихся того, что предлагает нам природа, и насколько невозможна настоящая философия без помощи геометрии, в соответствии с истиной, провозглашённой Платоном.

Г. Галилей

Работы Галилео Галилея

На протяжении XVI в. закладывался фундамент здания современной науки, превратившегося потом в поражающий своим величием небоскрёб. К этому приложили усилия многочисленные мыслители, жившие преимущественно в Италии, так как именно из этой страны стали проникать в Европу идеи Возрождения. Там же, в итальянском городе Пизе, родился и долгое время работал великий учёный, про которого можно сказать, что именно он завершил закладку фундамента и начал возводить само здание науки. Этим человеком был Галилео Галилей (1564–1642) (рис. 16). В юные годы Галилей изучал медицину, однако затем увлёкся наблюдениями за движущимися предметами. Движение – вот что в первую очередь интересовало основателя физики. Как мы знаем, движение почти за две тысячи лет до того изучал и Аристотель, но Галилей пришёл к совершенно противоположным выводам.

Рис. 16. Галилео Галилей

По поводу ранних исследований Галилея ходит много легенд, большинство из которых нельзя достоверно подтвердить. Говорят, что ещё в ранней молодости он бросал различные предметы с наклонной Пизанской башни, определяя время их падения путём подсчёта ударов своего пульса, и таким образом заметил, что ускорение не зависит от массы предметов (рис. 17). Это был серьёзный удар по представлениям Аристотеля, принимавшимся в то время за абсолютную истину.

Рис. 17. Пизанская башня известна во всём мире. Она достигает в высоту 55 м, а надпись на ней свидетельствует о том, что она заложена в 1174 г. В 1564 г. в Пизе родился Галилео Галилей, будущий знаменитый учёный

Вспомним утверждение Аристотеля о том, что каждое тело стремится к своему месту, зависящему от соотношения входящих в это тело элементов. Опровергая это учение, Галилей замечал, что если тела будут двигаться не в воздухе, а в воде, то, например, дерево, которое считают тяжёлым, становится лёгким, потому что движется вверх. Галилей также показал, что если бы не существовало сопротивления воздуха, то все предметы падали бы с одинаковым ускорением. Собственно говоря, об этом обстоятельстве догадывались и раньше – понятно, что парашют, изобретённый Леонардо да Винчи, не уменьшает массы человека, но замедляет его падение, – но Галилей впервые высказал это положение в виде строгого принципа.

Вообще выводы Галилея часто противоречили повседневному человеческому опыту, например это касается принципа инерции. Аристотель утверждал, и это казалось всем очевидным, что скорость движения тела зависит от приложенной к нему силы. Галилей же доказывает, что движение будет происходить с постоянной скоростью, если на него не действует никакая сила. Интересно, что к этому выводу Галилей пришёл с помощью рассуждений, напоминающих доказательство от противного в математике: поскольку наклон плоскости, по которой движется тело, ускоряет его движение вниз и замедляет движение вверх, то при отсутствии этого наклона, т. е. на горизонтальной плоскости, скорость движения вообще не должна меняться.

Ясно, что закон инерции противоречит всем реально наблюдаемым явлениям, – все знают, что всякий движущийся предмет, если его не подталкивать, довольно скоро остановится. И Галилей разрешает это противоречие с помощью того же аргумента, который он использовал для объяснения падения предметов: закон соблюдался бы в точности, если бы не существовало сопротивления среды. В том, что среда имеет отношение к замедлению движения, легко убедиться. Для этого надо подтолкнуть один и тот же предмет с одной и той же силой сначала по стеклу, а потом по мягкой ткани и убедиться в том, что во втором случае он остановится гораздо быстрее. Но всё-таки что значит «если бы…»? Ведь на самом деле не может быть так, чтобы сопротивление среды (трение, как мы его теперь называем) вообще отсутствовало. И здесь мы сталкиваемся с одним из основополагающих принципов науки – абстракцией, или абстрагированием.

Абстракция и идеализация.

Абстракцией называют мысленное выделение в каждом явлении наиболее значимых его свойств и отвлечение (абстрагирование) от тех, которые кажутся несущественными. Без абстракции невозможно никакое научное исследование, ведь в природе не бывает двух абсолютно одинаковых объектов. Нельзя изучать законы движения, если учитывать все выпуклости и зазубрины на каждом камне. Нельзя делать заключений в биологии или психологии, если учитывать тот факт, что каждое животное и тем более человек имеет свои индивидуальные особенности. Поэтому приходится абстрагироваться от многого из того, что мы наблюдаем. Высшую степень абстрагирования называют идеализацией. В процессе исследования реально существующих предметов создаются образы мысленных объектов, которые не только не существуют, но и не могут реально существовать в природе. Такими идеализированными объектами являются, например, материальная точка, идеальный газ, геометрические фигуры и тела. Создание таких объектов является началом процесса моделирования, о котором мы будем говорить в дальнейшем, когда вместо реальных объектов используются их идеальные модели.

Может показаться, что метод абстракции и идеализации отдаляет исследование от реальности и ведёт к изучению явлений, не существующих в природе. Но вся история науки показывает, что именно правильное использование абстракции позволило открыть самые объективные явления и привело к абсолютно реальным техническим достижениям. Именно пренебрежение формой, а часто и размерами предметов, силой трения и многими другими факторами позволило Галилею, Ньютону и их последователям разработать точную механику, а впоследствии и другие разделы естествознания.

Высшей степенью абстракции Галилей считал математику, так как только она может выразить явления в идеальном виде, освобождённом от случайных погрешностей. Ни один циркуль не способен изобразить абсолютно правильную окружность, но выражение «окружность есть геометрическое место точек, равноудалённых от точки, называемой центром» и соответствующее ему уравнение характеризуют её абсолютно точно. Только с помощью математики, как полагал Галилей, можно нарисовать правильную картину Мира. Он считает, что книга природы

«написана на языке математики, её буквами служат треугольники, окружности и другие геометрические фигуры, без помощи которых человеку невозможно понять её речь; без них – напрасное блуждание в тёмном лабиринте».

Со времени Галилея в научный обиход вошли понятия абстрагирования, эксперимента, измерения и математической обработки результатов. В следующих параграфах мы рассмотрим, в чём состоит их суть.

Проверьте свои знания

1. Что утверждает открытый Галилеем закон инерции?

2. От чего абстрагировался Галилей, формулируя закон инерции?

3. С помощью каких экспериментов Галилей доказал, что, если на тело не действует сила, оно будет двигаться с постоянной скоростью?

Задания

1. Подготовьте доклад о жизни и научной деятельности Галилео Галилея.

2. Приведите примеры абстрагирования в различных науках.

3. Если у вас в школе имеется достаточно большой сосуд и насос, позволяющий откачивать воздух из этого сосуда, поместите в сосуд предметы различной формы и массы, а затем откачайте из него воздух (рис. 18). После этого переверните сосуд и убедитесь в том, что все предметы падают одновременно.

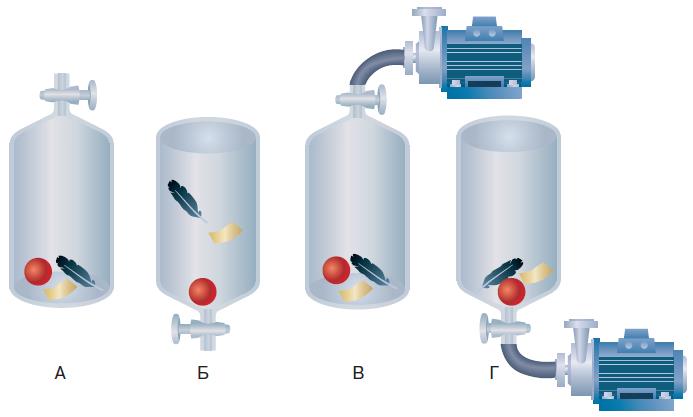
Рис. 18. Опыт с сосудом, на дне которого лежат тяжёлый шарик, кусок картона и перо: А – сосуд с воздухом; Б – при переворачивании сосуда все предметы падают по-разному и достигают дна сосуда в разное время; В – из сосуда откачали воздух; Г – при переворачивании все предметы одновременно оказываются на дне сосуда