Глава 7 ВЛИЯНИЕ ВЕТРА НА ПОЛЕТ САМОЛЕТА
§ 58. ЭЛЕМЕНТЫ ПОЛЕТА В БЕЗВЕТРИЕ
В неподвижном воздухе, т. е. при безветрии, направление движения самолета относительно земной поверхности совпадает с направлением его продольной оси, а скорость передвижения равна воздушной скорости. Чтобы совершить полет из пункта А в пункт Б, достаточно направить продольную ось самолета на пункт Б и точно выдерживать взятый курс (рис. 130).

Рис. 130. Движение самолета в воздухе в условиях полного безветрия
В безветрие навигационным элементом полета является вектор воздушной скорости самолета v. Величина вектора воздушной скорости зависит от режима работы двигателя самолета, высоты и плотности воздуха. И чем больше будет вектор воздушной скорости самолета, тем меньше потребуется путевого времени (t) для покрытия расстояния между пунктами А и Б. Путевое время t определяется по формуле
t = S·60/V
где t — путевое время в минутах;
S — длина пути между пунктами в км;
V — воздушная скорость в км/час.
Пример. Воздушная скорость самолета = 160 км/час. Расстояние между пунктами А и Б = 50 км.
Определить путевое время t.
Решение. Подставляем значения в формулу, получим
t = 50·60/160 = 19 мин
Эту же задачу можно решить с помощью НЛ-8 по ключу (рис. 131).

Рис. 131. Ключ для определения на НЛ-8 — путевого времени по S и V
На шкале линейки «Путевая скорость» находим деление 160 и против него устанавливаем треугольный индекс. На шкале «Пройденное расстояние» находим деление 50 и против него на шкале «Время» читаем искомое время — 19 мин.
В практике самолетовождения почти никогда не бывает полета в полном безветрии, так как атмосфера никогда не находится в состоянии полного покоя. Воздушные массы постоянно передвигаются в горизонтальном и вертикальном направлениях. Горизонтальное передвижение воздушных масс называется ветром.
Ветер как по величине, так и по направлению не является постоянным и меняется с изменением расстояния, высоты полета и времени. Скорость ветра V измеряется в километрах в час, а его направление δ в градусах от 0 до 360° от северного направления меридиана в сторону хода часовой стрелки.
При навигационных расчетах принято брать направление ветра «Куда дует», т. е. направление (точка на горизонте), в которую дует ветер, в отличие от метеорологического «Откуда дует».
Направление навигационного ветра отличается от направления метеорологического на величину 180°.
Для того чтобы перевести метеорологическое направление ветра в навигационное или обратно, необходимо к известному направлению ветра прибавить или вычесть из него 180° по формуле
δнав= δмет ± 180 — (±ΔМ),
где δнав— навигационное направление ветра;
δмет — метеорологическое направление ветра;
ΔМ — магнитное склонение в районе измерения ветра.
§ 59. ЭЛЕМЕНТЫ ПОЛЕТА В ПЛОСКОСТИ ВЕТРА (с попутным ветром)
Все, что находится в среде воздушной массы, передвигается вместе с ней. Так, например, аэростат, находясь, в воздухе, переносится воздушной массой в направлении ее движения со скоростью, равной скорости ветра, т е. перемещается относительно поверхности земли со скоростью ветра. Воздушная же скорость аэростата равна нулю. Навигационными элементами полета аэростата будут являться скорость и направление ветра (рис. 132).

Рис. 132. Движение аэростата в воздухе при ветре
Движение самолета с попутным ветром несколько напоминает нам картину движения аэростата в воздушной массе, но с той разницей, что самолет под действием воздушной скорости перемещается в направлении своей продольной оси. в то же время скорость воздушного течения увлекает самолет в направлении движения ветра. В результате этого получается сложение векторов: вектора воздушной скорости самолета и вектора ветра (рис. 133).

Рис. 133. Полет самолета при попутном ветре
Сложение этих векторов дает нам новое значение скорости, т. е. путевую скорость самолета W.
Путевая скорость при движении самолета с попутным ветром определяется формулой
W = V + U.
Путевой скоростью самолета называется скорость перемещения самолета относительно поверхности земли.
Путевая скорость является геометрической суммой воздушной скорости, скорости ветра и зависит от их величины и направления. Не трудно понять, что при движении самолета в условиях попутного ветра имеется три навигационных вектора, направленных по одной линии: вектор воздушной скорости самолета, вектор ветра, направленный по линии продольной оси самолета, образующий суммарный вектор, и вектор путевой скорости самолета (результирующий).
Путевая скорость самолета является одним из важных навигационных элементов полета, без знания которого нельзя точно вести контроль пути по дальности.
Путевая скорость при попутном ветре может быть определена двумя способами:
— по воздушной скорости и скорости ветра;
— по времени полета и расстоянию.
Пример. Воздушная скорость 160 км/час. Ветер попутный, 30 км/час.
Определить путевую скорость самолета по формуле
W = 160 + 30 = 190 км/час.
По известным времени полета и расстоянию путевая скорость рассчитывается по формуле
W = S·60/t
где W — путевая скорость самолета в км/час;
S — пройденное расстояние в км;
t — время полета в минутах.
Пример. Расстояние S = 80 км, время полета самолета t = 25 мин.
Определить путевую скорость самолета.
Решение.
W = 80·60/25 = 192 км/час.
Путевую скорость по известным S и t можно рассчитать на НЛ-8 по ключу (рис. 134).

Рис. 134. Определение на НЛ-8 путевой скорости самолета по S и t:
а — ключ для решения; б — решение
Направление движения самолета относительно земной поверхности в условиях попутного ветра совпадает с направлением его продольной оси. Чтобы совершить полет из пункта А в пункт Б, достаточно направить продольную ось самолета на пункт Б и выдерживать заданный курс.
§ 60 ЭЛЕМЕНТЫ ПОЛЕТА В УСЛОВИЯХ ВСТРЕЧНОГО ВЕТРА
Движение самолета в условиях встречного ветра обусловлено непрерывным воздействием вектора ветра, направленного навстречу движению самолета. Равнодействующая двух скоростей — воздушной скорости самолета и скорости ветра, действующих по одной прямой и направленных в противоположные стороны, равна их разности и направлена в сторону воздушной скорости. Эта равнодействующая и является путевой скоростью самолета (рис. 135).
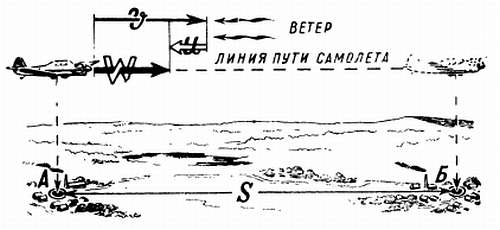
Рис. 135. Полет самолета при встречном ветре
При встречном ветре путевая скорость самолета определяется по формуле
W = V — U.
Пример. Воздушная скорость самолета 160 км/час. Скорость встречного ветра 30 км/час.
Определить путевую скорость самолета.
Решение.
W = 160 — 30 = 130 км/час. Это значит, что самолет движется (летит) относительно поверхности земли со скоростью 130 км/час.
Пример. Расстояние между пунктами А и Б, равное 80 км, самолет пролетел за 37 мин.
Определить путевую скорость по формуле и на НЛ-8.
Решение.
W = 80·60/37 = 130 км/час
На навигационной линейке НЛ-8 путевую скорость самолета определяют по времени пролета расстояния (рис. 136).

Рис. 136. Определение на НЛ-8 путевой скорости
Встречный ветер, так же как и попутный, изменяет только величину путевой скорости, но не оказывает никакого влияния на боковое смещение самолета. Движение самолета относительно земной поверхности совпадает с направлением продольной оси самолета. Движение самолета в условиях встречного ветра обусловлено тремя навигационными векторами: вектором воздушной скорости самолета, вектором ветра и вектором путевой скорости, который всегда меньше вектора воздушной скорости на величину вектора ветра.
§ 61. ЭЛЕМЕНТЫ ПОЛЕТА С БОКОВЫМ ВЕТРОМ
При полете без ветра, строго по ветру или против ветра земные предметы перемещаются обратно направлению полета и вдоль продольной оси самолета. При боковом ветре или при попутно-боковом, встречно-боковом ветре земные предметы уходят от направления продольной оси самолета назад и в сторону: влево — при ветре, дующем в левый борт самолета, вправо — при ветре, дующем в правый борт. Что же произойдет, если не учитывать в полете боковой ветер? На рис. 137 показано движение самолета в условиях бокового ветра, когда летчик, не зная скорости и направления ветра, направил продольную ось самолета из точки А в точку Б с задачей вывести самолет в эту точку.
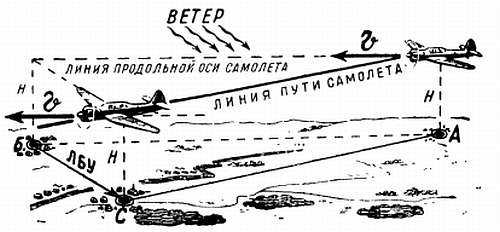
Рис. 137. Полет самолета при боковом ветре
Если бы не было бокового ветра, самолет оказался бы через определенный промежуток времени над точкой Б. При боковом ветре этого не произойдет. Самолет под действием воздушной скорости будет перемещаться в направлении своей продольной оси, в то время как скорость воздушного течения увлекает его в сторону от этого направления. В результате сложения этих движений самолет переместится по равнодействующей, построенной на скоростях самолета и ветра. Таким образом, самолет совершает движение не по линии продольной оси, а по линии фактического пути самолета и через какой-то промежуток времени окажется над точкой С, уклонившись от линии заданного пути (от точки Б) на величину линейного бокового уклонения (ЛБУ).
Итак, действительное перемещение самолета, участвующего одновременно в двух движениях — вектора воздушной скорости и вектора ветра, направленные под углом друг к другу, происходит по диагонали параллелограмма, построенного на векторах этих движений. Получается навигационный треугольник скоростей (рис. 138).
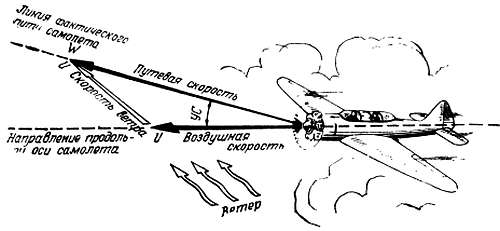
Рис. 138. Навигационный треугольник скоростей
Сторонами этого треугольника являются векторы воздушной скорости, ветра и путевой скорости.
Угол, составленный вектором воздушной скорости и вектором путевой скорости, называется углом сноса и обозначается буквами УС. Если самолет сносит вправо относительно направления полета, УС будет положительным (+УС) и наоборот.
Если через основание навигационного треугольника провести меридианы, получим ряд дополнительных навигационных элементов, показанных на рис. 139.

Рис. 139. Навигационный треугольник скоростей, ориентированный относительно меридиана
Элементы в навигационном треугольнике скоростей следующие:
V — воздушная скорость самолета, измеряется в км/час.
U — скорость ветра, измеряется в км/час.
W — путевая скорость, измеряется в км/час.
К — курс самолета — угол, заключенный между северной частью меридиана и вектором воздушной скорости самолета.
ПУ — путевой угол самолета — угол, заключенный между северной частью меридиана и вектором путевой скорости или линией пути самолета.
УС — угол, заключенный между вектором (продольной осью самолета) воздушной скорости самолета и вектором путевой скорости или линией пути самолета.
δ — направление ветра — угол, заключенный между северной частью меридиана и направлением вектора ветра.
УВ — угол ветра — угол между линией пути и направлением ветра.
§ 62. ИЗМЕНЕНИЕ ЭЛЕМЕНТОВ НАВИГАЦИОННОГО ТРЕУГОЛЬНИКА СКОРОСТЕЙ
Элементы навигационного треугольника находятся в определенной зависимости между собой.
Изменение одних элементов вызывает изменение других. Величина угла сноса зависит от воздушной скорости самолета, скорости ветра и угла ветра. Например, у скоростных самолетов величина угла сноса меньше, чем у самолетов, имеющих малую воздушную скорость при одном и том же ветре. Чем больше скорость бокового ветра, тем больше угол сноса.
Величина путевой скорости зависит от величины воздушной скорости, скорости ветра и угла ветра. Максимальная путевая скорость будет при угле ветра, равном нулю; минимальная путевая скорость будет при угле ветра, равном 180°. Путевая скорость равна воздушной скорости, когда угол ветра приближенно равен 90°.
Изменение навигационных элементов полета от изменения скорости и угла ветра (УВ). На приведенных трех рисунках навигационного треугольника скоростей видна зависимость навигационных элементов полета от изменения скорости и угла ветра.
На рис. 140, а показан навигационный треугольник скоростей, рассчитанный на основе данных скорости и направления ветра и заданной воздушной скорости. Если скорость и угол ветра в полете будут такими же величинами, как и расчетные, то рассчитанные элементы полета ПУ, К, УС и V также будут равны фактическим элементам полета, и самолет будет выведен в заданную точку маршрута в точно рассчитанное время без уклонений.
В практике самолетовождения летчик может встретиться с случаями в полете, когда расчетные данные полета по известной скорости и направлению ветра не соответствуют фактическим данным. Такое несоответствие обнаруживается тогда, когда самолет уклоняется от заданной линии пути, в то время как расчетные навигационные элементы полета — курс, воздушная скорость — выдерживаются.
На рис. 140, б показана схема навигационного треугольника скоростей, когда фактическая скорость ветра в полете оказалась больше расчетной на величину ΔU. В результате изменились навигационные элементы треугольника, произошло увеличение ПУ, УС и W.
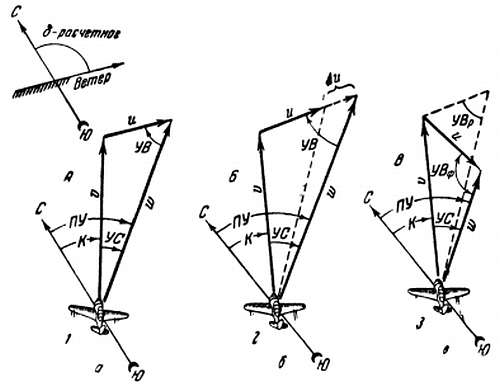
Рис. 140. Изменение навигационных элементов полета при изменении скорости и угла ветра (УВ):
а — расчетные элементы навигационного треугольника скоростей; б — фактическая скорость ветра оказалась больше расчетной на величину ΔU: произошло изменение элементов навигационного треугольника; в — фактический угол ветра оказался больше расчетного; произошло изменение элементов треугольника
В третьем примере (рис. 140, в) схема изображает изменение угла ветра (УВ), вследствие чего явилось изменение навигационных элементов треугольника. В данном примере произошло незначительное увеличение ПУ и УС, в то время как W оказалась значительно меньше расчетной.
Изменение навигационных элементов треугольника от изменения воздушной скорости самолета. На изменение элементов навигационного треугольника может в значительной степени влиять изменение воздушной скорости полета вследствие невыдерживания летчиком скорости по прибору (рис. 141).

Рис. 141. Изменение навигационных элементов полета при невыдерживанни летчиком заданной воздушной скорости:
а — навигационный треугольник скоростей при заданной V; б — скорость выдерживалась меньше заданной на ДУ; в — скорость выдерживалась больше заданной на ДУ
На рис. 141, б показано уменьшение воздушной скорости самолета по отношению к расчетной на ΔV. Уменьшение V привело к изменению ПУ и УС в сторону их увеличения. Путевая скорость уменьшилась на эту же величину. На рис. 141, в показано увеличение ΔV по сравнению с расчетной на V. Все это привело к тому, что ПУ и УС фактически оказались меньше расчетных, а путевая скорость увеличилась по сравнению с расчетной на величину ДК.
Таким образом, чтобы пролететь в заданном направлении АБ необходимо всегда учитывать влияние ветра в полете и направлять продольную ось самолета так, чтобы его фактический путевой угол следования был по величине равен заданному путевому углу (ЗПУ), т. е. фактический путь следования совпадал бы с заданной линией пути. Знание ветра в полете, т. е. фактического угла сноса, дает возможность всегда определить путевой угол самолета. Для этого необходимо к курсу самолета алгебраически прибавить угол сноса. Найденный в полете путевой угол называется фактическим путевым углом (ФПУ) (рис. 142).

Рис. 142. Движение самолета по линии заданного пути
Курс самолета, взятый с учетом угла сноса, называется курсом следования (КС). Если отсчет углов производится от магнитного меридиана, тогда ФПУ будет иметь название ФМПУ (фактический магнитно-путевой угол), курс следования — МК = ЗМПУ — (±УС).
Пример. Какой необходимо взять МК из точки А для полета в точку Б, если ЗМПУ = 102°. Как видно на схеме, ветер дует в левый борт самолета, значит пролетаемые ориентиры на поверхности земли будут уходить влево, УС положительный и равен +8°. Определить МК.
Решение. МК = ЗМПУ — (±УС); МК = 102°— (+8°) = 94°. При условии постоянного ветра, точного выдерживания курса и воздушной скорости самолет будет двигаться по линии заданного пути; тогда ФМПУ будет равняться ЗМПУ.
§ 63. ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ ПОЛЕТА
Определение курса следования, угла сноса и путевой скорости можно произвести графически на листке бумаги в следующем порядке:
1. Провести прямую (меридиан), концы ее обозначить буквами См и Юм, на середине отметить точку, обозначающую точку вылета.
2. Из точки вылета при помощи транспортира отложить заданный магнитный путевой угол и провести линию пути произвольной длины (рис. 143).
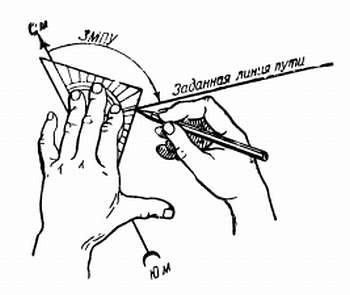
Рис. 143. Прокладка заданного магнитного путевого угла
3. Из точки вылета отложить в каком-либо масштабе вектор скорости ветра в направлении «Куда дует» ветер (рис. 144).

Рис. 144. Прокладка вектора скорости ветра
4. С конца вектора скорости ветра в том же масштабе, в котором откладывался вектор скорости ветра, радиусом, равным истинной воздушной скорости, при помощи масштабной линейки сделать засечку на линии пути (рис. 145).

Рис. 145. Откладывание вектора истинной воздушной скорости в масштабе
5. Сделанную засечку на линии пути соединить прямой с концом вектора скорости ветра, продолжив ее до пересечения с меридианом (рис. 146).

Рис. 146. Вектор воздушной скорости (пунктир) продлен до меридиана
6. Транспортиром измерить угол между меридианом и линией воздушной скорости. Этот угол и есть магнитный курс следования. Затем определить угол сноса по правилу: угол сноса равен путевому углу минус курс: УС = ПУ — МК, или измерить его транспортиром.
7. Пользуясь линейкой, тем же масштабом, в котором откладывали скорость ветра и воздушную скорость, измерить отрезок линии пути от точки вылета до засечки на линии пути; получится величина путевой скорости.
Рассчитанный таким способом курс следования (МКсл), с которым самолет отойдет от точки А, обеспечит движение самолета по линии заданного пути.
Пример. Заданный магнитный путевой угол = 90°. Истинная воздушная скорость 170 км/час. Ветер на высоте полета по шаропилотным наблюдениям: направление δаэр = 320°, скорость ветра U = 30 км/час, магнитное склонение ΔМ = +5°.
Определить графически магнитный курс следования, угол сноса и путевую скорость.
Решения: 1. Перевести шаропилотный ветер в аэронавигационный, т. е. «Куда дует» ветер; получим 320°— 180°— (+5°) = 135°.
2. На листе бумаги произвести графическое построение и определить неизвестные величины. Масштаб — 15 км в 1 см (рис. 147).
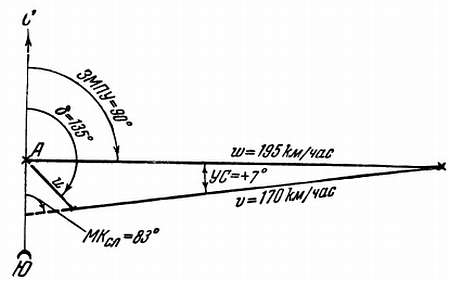
Рис. 147. Измерение на схеме MKcл, УС и W
§ 64. НАЗНАЧЕНИЕ И УСТРОЙСТВО ВЕТРОЧЕТА
Ветрочет предназначен для графического решения задач по определению элементов навигационного треугольника скоростей. Ветрочет состоит из сектора, азимутального круга и линейки (рис. 148).

Рис. 148. Ветрочет
По дуге сектора в обе стороны от осевой линии, отмеченной цифрой 0, называемой курсовой чертой, нанесена шкала сноса с ценой деления 1°. На осевой линии имеется прорезь для закрепления на ней азимутального круга, который имеет шкалу, разделенную на 360°. На поверхности круга имеется ряд концентрических окружностей, обозначающих скорость ветра в десятках километров в час. Азимутальный круг имеет свободное вращение вокруг своей оси.
Линейка вращается около вершины угла сектора и перемещается другим концом по дуге шкалы сносов. На линейке нанесена шкала скоростей в километрах в час.
§ 65. ОПРЕДЕЛЕНИЕ НА ВЕТРОЧЕТЕ КУРСА СЛЕДОВАНИЯ, УГЛА СНОСА И ПУТЕВОЙ СКОРОСТИ
Определение курса следования, угла сноса и путевой скорости ветрочетом производится в следующем порядке:
1. Найти на линейке скоростей ветрочета деление, соответствующее заданной истинной воздушной скорости, и против него установить центр азимутального круга ветрочета (рис. 149).

Рис. 149. Центр лимба ветрочета, установленный против заданной истинной скорости самолета
2. На азимутальном круге найти деление, соответствующее навигационному направлению ветра на высоте полета («Куда дует»), вращением круга установить его против курсовой черты. Пользуясь концентрическими окружностями на азимутальном круге и делениями линейки скоростей, отложить от центра вектор скорости ветра, обозначив конец вектора линией со стрелкой (рис. 150).

Рис. 150. Нанесение вектора ветра на лимбе
3. На азимутальном круге найти деление, соответствующее заданному магнитному путевому углу (ЗМПУ), и, вращая круг, установить его против курсовой черты ветрочета. Линейку скоростей установить на 0 шкалы сносов, прочертить простым карандашом диаметр, отметить направление полета самолета стрелкой.
4. Линейку скоростей правой ее стороной (рабочей) установить на точку ветра и вращением азимутального круга добиться параллельности с прочерченным диаметром, причем стрелка его должна быть направлена вверх.
5. Отсчитать против курсовой черты на азимутальном круге магнитный курс следования: по первой стороне линейки (на шкале сносов) — угол сноса; против точки ветра (на линейке скоростей) — путевую скорость (рис. 151).
Рис. 151. Отсчет МК, УС и W на ветрочете
Пример. Заданный магнитный путевой угол ЗМПУ = 190°. Заданная истинная воздушная скорость Vист = 190 км/час.
Ветер на высоте полета по шаропилотным наблюдениям: направление δаэр = —265°, скорость U = 20 км/час, магнитное склонение ΔМ = +2°.
Определить магнитный курс следования, угол сноса и путевую скорость.
Решение. На линейке скоростей ветрочета находим деление 190 км/час и против него устанавливаем центр азимутального круга. На азимутальном круге находим деление 190°, устанавливаем его против курсовой черты и проводим диаметр на азимутальном круге. Переводим шаропилотный ветер в навигационный («Куда дует») и получаем δнав = 265°— 180° — (+2°) = 83°.
На азимутальном круге наносим вектор ветра (скорость и направление ветра). Добиваемся параллельности с диаметром на азимутальном круге. Затем против курсовой черты отсчитываем магнитный курс следования 197°. На шкале сносов, по правой стороне линейки, читаем угол сноса — 7°, а против точки ветра на линейке скоростей — путевую скорость — 183 км/час.
§ 66. РАСЧЕТ УГЛА СНОСА, ПУТЕВОЙ СКОРОСТИ И КУРСА СЛЕДОВАНИЯ НА НАВИГАЦИОННОЙ ЛИНЕЙКЕ НЛ-8 И В УМЕ
Расчет угла сноса и путевой скорости может быть выполнен при помощи навигационной линейки НЛ-8.
Для расчета нужно знать:
— истинную воздушную скорость (Vист);
— заданный магнитный путевой угол (ЗМПУ);
— угол ветра и скорость ветра (УВ и U).
Углом ветра (УВ) называется угол между вектором путевой скорости и вектором скорости ветра. Угол ветра отсчитывается от вектора путевой скорости по ходу часовой стрелки от 0° до 360° (рис. 152).
Рис. 152. Отсчет угла ветра
Угол ветра равен направлению ветра минус путевой угол, т. е. УВ = δ — ПУ.
При расчете угла сноса и путевой скорости нужно пользоваться нижней шкалой «Синусы». Для этого необходимо запомнить следующие правила:
а) угол ветра считать меньше 180°:
— если угол ветра получается в пределах от 90° до 180°, его нужно вычесть из 180°;
— если угол ветра получается в пределах от 180° до 270°, его нужно вычесть из 270°;
— если угол ветра получается в пределах от 270° до 360°, его нужно вычесть из 360°.
б) При определении знака угла сноса:
— если угол ветра получается в пределах от 0° до 180°, угол сноса имеет знак плюс (+);
— если угол ветра получается в пределах от 180° до 360°, угол сноса имеет знак минус (—).
в) При определении путевой скорости:
— если угол ветра получается в пределах от 0° до 90° и от 270° до 360°, то полученный угол сноса нужно прибавлять к величине угла ветра;
— если угол ветра получается в пределах от 90° до 180° и от 180° до 270°, то полученный угол сноса нужно вычесть из величины угла ветра;
— если угол ветра получается 90° или 270°, то путевая скорость равна воздушной (W = V);
— если угол ветра получается то путевая скорость равна сумме воздушной скорости и скорости ветра (W = V + U); — если угол ветра получается 180°, то путевая скорость равна разности воздушной скорости и скорости ветра (W = V — U).
Пример. Истинная воздушная скорость 200 км/час. Угол ветра 60°. Скорость ветра 40 км!час. Заданный магнитный путевой угол 100°.
Определить угол сноса, путевую скорость и магнитный курс следования.
Решения:
1. Определение угла сноса. На шкале линейки «Расстояния» находим деление, соответствующее истинной воздушной скорости — 200 км/час, и против него устанавливаем визир. На шкале «Синусы» находим деление, соответствующее углу ветра 60°, и совмещаем его с воздушной скоростью 200 км/час. На шкале «Расстояния» находим деление, соответствующее скорости ветра 40 км/час, и против него устанавливаем визир, затем на шкале «Синусы» против визира читаем искомый угол сноса 10° (если угол сноса получается меньше 5°, то отсчет производится по шкале «Тангенсы»). В нашем примере угол ветра лежит в пределах 90—180° и полученный угол сноса имеет знак плюс (+10°) (рис. 153).

Рис. 153. Определение на НЛ-8 угла сноса по истинной воздушной скорости и углу ветра
2. Определение путевой скорости. Не сдвигая установленный визир (на U и УС), алгебраически прибавляем угол сноса к углу ветра (УВ + УС); получим: 60°+ (+10°) =70°.
Визир устанавливаем на шкале «Синусы» на полученную сумму 70° и на шкале «Расстояния» против визира читаем искомую путевую скорость, равную 223 км/час (рис. 154).
Рис. 154. Определение на НЛ-8 путевой скорости по углу сноса, скорости и сумме значений угла ветра и угла сноса
3. Определение магнитного курса следования. Для этого из данного магнитного путевого угла алгебраически вычитаем угол сноса, получаем искомый магнитный курс следования: 100°— (-10°) = 90°.
Решение. УС = +10°, W = 223 км/час и МКслед. = 90°.
Пример. Vист = 180 км/час, УВ = 220°, U = 30 км/час и ЗМПУ = 15°.
Определить УС, W и МКслед..
Решение. Определяем УС. Угол ветра 220° находится в пределах между 180° и 270°; поэтому по вышеприведенному правилу УВ = 270–220° = 50°.
Затем производим решение по НЛ-8, получаем УС = 7°.
Так как УВ получается в пределах от 180° до 360°, то УС будет иметь минусовой знак, т. е. УС = —7°.
Определяем W.
Полученный угол сноса (УС — 7°) вычитаем из величины угла ветра: 50° + (—7°) = 43°.
Производим решение по НЛ-8, получим W = 191 км/час.
Определяем МКслед.. МКслед. = ЗМПУ — (+УС) = 15°— (—7°) = 22°.
УС = — 7°; W = 191 км/час и МКслед. = 22°.
§ 67. ОПРЕДЕЛЕНИЕ НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ ПОЛЕТА В УМЕ
Расчет путевой скорости и курса следования приближенно в уме. Для этого необходимо прежде всего запомнить следующие правила:
1. При отсутствии ветра, когда U = 0 и при ветрах строго боковых, когда угол ветра УВ = 90° или 270°, путевая скорость W равна воздушной скорости: W = Vист.
2. При попутном ветре (УВ = 0) путевая скорость равна
W = Vист + U.
3. При встречном ветре (УВ = 180°) путевая скорость равна
W = Vист — U.
4. При других направлениях ветра, начиная с 10° УВ, величина путевой скорости зависит от скорости ветра и величины угла ветра. Максимальный угол сноса определяется по формуле
УСмакс = U·60/V
Для расчета путевой скорости курса следования приближенно в уме можно пользоваться табл. 1.
При пользовании таблицей необходимо определить угол ветра по формуле
УВ = δ — МПУ.
Знак угла сноса определяется в зависимости от того, с какой стороны относительно направления движения самолета дует ветер. Если ветер дует справа — снос отрицательный, если слева — снос положительный.
Пример. Истинная воздушная скорость 210 км/час, скорость ветра 36 км/час, направление ветра 140°. Заданный магнитно-путевой угол 80°. Девиация компаса +5°. Определить путевую скорость.
Решения: 1. Определяем угол ветра:
УВ = δ — ЗМПУ = 140°— 80° = 60°.
2. Определяем УСмакс
УСмакс= U·60/V = 39·60/210 ~= 10°
3. Определяем УС. Пользуясь таблицей 1, УС рассчитываем по формуле
УС = (3/4)·УСмакс = (3/4)·10°= +7° (ветер слева).
4. Определяем МК:
МК = ЗМПУ — (±УС) = 80° — (+7°) = 73°.
КК = МК — (±ΔК) = 73°— (+5) = 68°.
Определение путевой скорости по пройденному расстоянию и времени полета подсчетом в уме. Порядок расчета следующий:
1. Измерить на карте пройденное расстояние за время полета от последней отметки МС.
2. Разделить пройденное расстояние на время, получить количество километров, пройденных за 1 мин.
3. Полученное число умножить на 60 мин., получим путевую скорость в км!час.
Пример. Самолет пролетел расстояние S = 24 км за 8 мин.
Определить путевую скорость.
Решение. 24:8 = 3 км/мин; W = 3·60=180 км/час.
Определение расчетного путевого времени подсчетом в уме можно производить двумя способами:
1) путем определения числа километров, проходимых самолетом в одну минуту;
2) определением части от целого, т. е. вычислением части пути, пройденного самолетом, относительно всей длины пути.
Пример 1. Самолет прошел расстояние 40 км за 13 мин.
Определить расчетное путевое время в уме для расстояния 80 км, 100 км и 160 км.
Решение. За 13 мин. самолет прошел 40 км и за 1 мин. 40:13 = 3 км.
Расчетное путевое время для 80 км будет: 80:3 = 26,8 мин ~= 27 мин., 100:3 = 33 мин., 160:3 = 53 мин.
Пример 2. Расстояние 20 км самолет прошел за 6 мин.
Определить расчетное путевое время для расстояния 90 км.
Решение. Расстояние 90 км, делим на 20 км, получаем 90:20 = 4,5. Полученную величину умножаем на время полета и получаем расчетное путевое время, равное 6·4,5 = 27 мин.
Определение в уме пройденного расстояния по скорости и времени полета. Этот способ расчета наиболее простой. От значения путевой (воздушной) скорости следует отбросить третью цифру; тогда получится расстояние, проходимое самолетом за 6 мин. Зная путь, проходимый самолетом за 6 мин., можно легко определить расстояние за любой промежуток времени.
Пример. Путевая скорость самолета W = 200 км/час.
Определить пройденное расстояние S за t = 22 мин.
Решение. Отбросив от значения путевой скорости третью цифру, находим: за 6 мин. самолет проходит путь 20 км, следовательно, за 18 мин. он пройдет: 20·3 = 60 км, за остальные 4 мин. — 13 км, а всего за 22 мин. проходит: 60 + 13 = 73 км.
Для облегчения решения задачи определения расстояния по известной скорости самолета и времени полета можно пользоваться табл. 2 или запомнить, сколько километров пути пролетит самолет в одну минуту.
Пример. W = 190 км/час, t = 9 мин. Определить S.
Решение. Находим в графе таблицы W = 190 км/час и в этой же графе проходимый путь самолетом за одну минуту, равный 3,2 км.
Получим: 3·9 = 27, 0,2·9 = 1,8 = 2 км, S = 27 + 2 = 29 км.
Расчет обратного магнитного курса следования. Иногда летчик вынужден прекратить выполнение задания и вернуться обратно на исходный пункт маршрута. В этом случае, зная угол сноса, который был на курсе следования, обратный курс рассчитывается по формуле.
МКобр = МКслед + 180 + (±2УС).
Пример. Магнитный курс следования к цели полета 290°, угол сноса —10°. Определить обратный магнитный курс.
Решение. МКобр = 290° + 180° + (—20°) = 90°.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК