Теория ценового мониторинга
Теория ценового мониторинга
Обобщим наше рассмотрение для случая произвольной мощности множества базисных товаров.
Соотношения между уместными ценами для случая, когда имеется n базисных товаров, будет иметь вид:
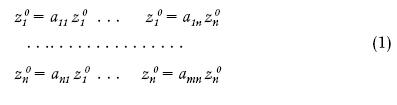
Соответственно и для интервала экономически обоснованных цен имеем систему неравенств:
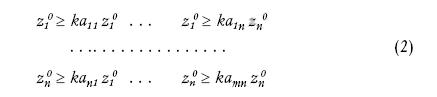
Система уравнений (1) создает в многомерном пространстве линию, которую мы также будем называть лучом уместных цен (ЛУЦ). Система уравнений (2) создает в многомерном пространстве {z1,z2… zn} конус допустимых цен. Таким образом, переход от простейшей модели двухмерного ценового пространства базисных цен к многомерному не приводит к новым явлениям, а лишь усложняет задачу и делает ее менее обозримой.
Мы видим, что вся информация о рынке базисных товаров содержится в системе коэффициентов
{a ik}, i,k = 1,2…, которые можно записать в виде матрицы A.
Матрица А называется матрицей ценовых паритетов, а коэффициент a ik этой матрицы – ценовым паритетом товара i по товару k. Смысл коэффициента a ik состоит в том, что он определяет, сколько единиц товара k необходимо отдать за единицу товара i при экономически равноправном обмене. Либо еще проще – во сколько раз единица товара i дороже единицы товара k.
Коэффициенты a ik не независимы, а подчиняются некоторым соотношениям. Эти соотношения легко получить из системы (1), если в уравнение для z 0i в зависимости от z0 j подставить значение z 0j в зависимости от z 0k и так делать сколь угодно долго, заканчивая подстановку величиной z 0i. Тогда мы получаем следующее условие на коэффициенты матрицы А:
aij aik . . . alm ami = 1 (4)
Это прямо следует из принципа паритета при обмене – если по этой матрице обменять некоторый товар на другой, второй товар на третий, третий на четвертый и т. д., то при любой длине цепочки обменов, возвратясь к исходному товару, мы получим то же самое его количество. Другими словами матрица паритетов A есть матрица с нулевой прибылью. Такие матрицы еще называются уравновешенными матрицами.
Матрица ценовых паритетов является частным случаем более общего типа курсовых матриц, широко используемых в финансовой и экономической науке и практике. Простейший пример – матрица валютных курсов. Отметим, что используются курсовые матрицы как с нулевой, так и с ненулевой прибылью, то есть как уравновешенные, так и неуравновешенные.
Матрица ценовых паритетов имеет значения 1 на главной диагонали. С точки зрения теории матриц матрица ценовых паритетов – это эрмитова матрица ранга 1.
Ранг 1 означает, что все ее строки и столбцы линейно зависимы, и для полного определения такой матрицы размерности n требуется знать не n(n-1), а лишь n-1 чисел.
Другими словами, зная лишь одну строку или один столбец, мы можем полностью восстановить матрицу ценовых паритетов. А зная уместную цену одного-единственно-го базисного товара и матрицу ценовых паритетов, мы восстанавливаем уместные цены для всего пула базисных товаров.
Таким образом, задача определения системы уместных цен базисных товаров раскладывается на две подзадачи:
1. Определить уместную цену хотя бы одного товара.
2. Определить матрицу ценовых паритетов.
Но как решать эти задачи, если калькуляционный подход не пригоден? Очевидно, что только по наблюдению самих рыночных цен товаров. Как мы уже
показывали ранее, при нестабильном рынке базисных товаров происходит постоянный инфляционный рост цен, но, кроме того, изображающая точка в ценовом пространстве при свободном рынке постоянно колеблется вокруг луча уместных цен. Таким образом, необходимо создать некоторый способ статистического анализа реальной рыночной ситуации, на основании которого и извлекать требуемую нам информацию.
В качестве исходных рыночных данных мы имеем зависимости цен базисных товаров от времени.
Интервал цен товаров слишком велик, и потому желательно привести все эти зависимости к одному масштабу. Это можно осуществить, если перейти от цен к индексам цен – индексам абсолютных цен базисных товаров:
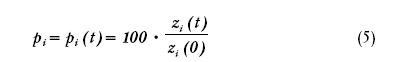
Индексы абсолютных цен удобны тем, что все цены приведены к одному масштабу, их можно нанести на один график. На дату начала наблюдения t 0 их значения для всех товаров равны 100 пунктам, а в дальнейшем они меняются в связи с инфляционным процессом.
А теперь найдем средневзвешенное значение индексов абсолютных цен:
Выбор весовых коэффициентов представляет не простую проблему. Желательно, чтобы они отражали важность товара в экономической структуре. Один из возможных вариантов использовать коэффициенты, пропорциональные объему продаж товара. Однако нередко в экономике используется и простейший выбор – все коэффициенты c j устанавливаются одинаковыми.
Отметим, что выбор способа взвешивания не является критичным. Результаты, получаемые при различных достаточно разумных выборах весовых коэффициентов, сравнительны близки друг к другу. Поэтому мы пока не будем подробно останавливаться на процедурах взвешивания. Этот индекс назовем интегральным индексом цен базисных товаров – ИИЦБТ.
ИИЦБТ во многом является характеристикой ценности национальных денег, точнее, динамики ценности денег, так как именно базисные товары являются определяющими в этом плане. И его можно использовать в качестве индикатора общей денежной инфляции. В настоящее время в качестве индикатора инфляции в России используется Индекс потребительских цен Госкомстата. Конечно, важность этого индекса трудно отрицать, особенно в социальном планировании и управлении. Но представляется не вполне корректным распространять процессы в области товаров потребительского назначения, более того, специфицированных для отражения уровня жизни прежде всего самых малоимущих слоев населения, на всю экономику. Ведь на основе Индекса цен Госкомстата Центробанк устанавливает ставки рефинансирования, правительство планирует бюджет и многое другое. И использование некорректного показателя является источником экономических трудностей во многих отраслях экономики, финансов, социальной жизни. Поэтому там, где использование госкомстатовского индекса корректно, там надо его использовать, например, в области пенсионного обеспечения, минимальной зарплаты и т. д. Но недопустимо абсолютизировать этот индекс, как бы ни была авторитетна организация, его ведущая. Там, где речь идет об общеэкономической ситуации, лучше использовать ИИЦБТ, в крайнем случае использовать совместно индекс цен потребительских товаров и индекс цен базисных товаров в качестве базы создания общеэкономического индекса.
Начальное значение P(0) равно 100 пунктам. Поэтому P(t) можно интерпретировать как индекс цен некоторого товара, начальная цена которого Z 0 =1, а цена Z(t) на момент времени t равна P(t). Этот товар можно назвать базисным комплексом. Он описывает как бы всю совокупность базисных товаров, некий комплексный обед на рынке-ресторане базисных товаров.
А теперь мы выскажем центральный постулат теории цен базисных товаров: цена базисного комплекса является уместной всегда.
Если все цены базисных товаров являются уместными, то и цена базисного комплекса также уместна. Если ценовая точка лежит вне луча уместных цен, то существует по крайней мере один товар, цена которого выше уместной, и по крайней мере один товар, цена которого ниже уместной. Поэтому при усреднении индексов абсолютных цен и создании таким образом базисного комплекса отклонение его цены от уместной будет по крайней мере меньше, чем у исходных товаров. Поэтому мы можем с хорошей достоверностью принять, что цена этого товара всегда лежит на луче уместных цен.
Этот постулат и позволяет дать простое и эффективное решение проблемы установления уместных цен.
Так как базисный комплекс есть базисный товар, то и для него верны соотношения (1).
Zy = atZ (7)
Здесь Z – базисный комплекс, значок «0» мы над ним не ставим, так как его цена всегда уместна. a i – ценовой паритет i-того товара по отношению к базисному комплексу. Этот ценовой паритет назовем главным ценовым паритетом для товара i. Совокупность {a1,a2… an} назовем главным вектором рынка базисных товаров.
Знание главного вектора позволяет легко определить матрицу обмена:
Из (8) следует:
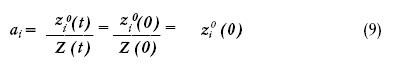
Рассмотрим теперь величину z i(t)/Z(t).
Произведем усреднение этого отношения по достаточно большому промежутку T.
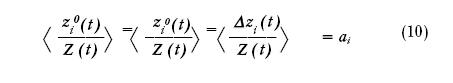
Второй член знакопеременный и при усреднении по периоду, существенно превышающему цикл движения цен, дает нуль. Здесь мы применили разложение цены z на уместную z0 и отклонение от уместной z = z-z0.
Введем теперь индексы относительных цен. Индекс относительных цен базисного товара равен отношению его индекса абсолютных цен к интегральному индексу цен базисных товаров.
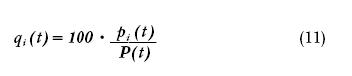
Индексы относительных цен дают наглядное представление сравнительной динамики относительного ценового движения. Рост этого индекса для некоторого товара означает опережающий рост цен данного товара по сравнению со средним ростом, падение его означает, что некоторый товар отстает в инфляционном движении. Индекс относительных цен дает динамику цен в так называемых «неизменных ценах», причем датой приведения является начало отсчета интегрального индекса инфляции. Подобного рода индексы под разными названиями широко используются в эконометрии.
Усредним значения индексов относительных цен по промежутку времени, существенно превышающем циклы ценового движения базисных товаров. Обозначим среднее индекса относительных цен через ‹q i›. Проанализируем, чему оно равно:
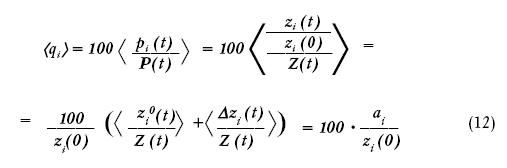
Отсюда получаем для главного ценового паритета:
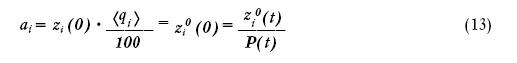
Таким образом, на основании ценового мониторинга мы получаем главный вектор цен, с помощью которого, используя отношения (8), легко получить и всю матрицу ценовых паритетов A = a ij.
Таким образом, задача определения матрицы ценовых паритетов базисных товаров определена полностью.
Отметим полезные соотношения:
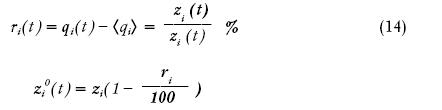
rt(t) дает отклонение реальной цены от уместной в процентах.
Вернемся вновь к смыслу индекса интегральной инфляции. Величина Z(t)=P(t) дает динамику изменения стоимости некоторого товара, который в принципе реально может быть предложен покупателю.
С другой стороны, величину
можно рассматривать как показатель, характеризующий динамику денег – Индекс покупательной силы (способности) денег.
В этой двойственности как раз и находит отражение специфика бумажных денег, отличающая их от золотых, абсолютных. В этом и есть специфика релятивистского денежного пространства, на котором разворачиваются экономические процессы.
Как легко понять, повышение цены базисного товара на q процентов лишь на долю q(l-Cj) идет на реальное повышение цены товара, а величина ctq идет на обесценение денег. Если же повышают одновременно к производителей на q процентов, то на повышение цен идет доля q(l – ?Kct), а остальное на обесценение денег. Таким образом, наиболее выгадывает тот, кто первым начинает повышение цен. Отсюда и следует стратегия борьбы с инфляционным движением – бить первого, кто высунется. Другими словами, от стратегии интегрального воздействия на всех участников процесса желательно перейти к стратегии выборочного, целевого воздействия и именно на того или тех, кто наиболее в данный момент «опасен».
Можно привести такой образный пример. Предположим движется пелотон велосипедистов, движение которого мы хотим затормозить. Вместо того чтобы запрещать двигаться быстро всем, накладывать на их колеса какие-то ограничители, гораздо проще направить на них встречную струю ветра. Тогда только первый будет встречать сопротивление воздуха, а остальные за его спиной будут двигаться совершенно свободно. И тем не менее движение замедлится, ибо как только кто-то выскочит вперед, так на него обрушивается сила ветра.
Параметр г, и есть параметр, по которому можно осуществлять воздействие. Установив пороговое значение
r › 0, при превышении которого воздействие осуществляется, мы тем самым установим конус цен, рекомендуемых государством.